概念
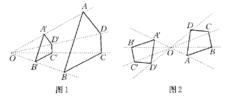 位似形
位似形位似形(homothetic figures)具有特殊位置的相似形。若兩個圖形F和F′的點之間可以建立一一對應關係,並且滿足:
1.連結任一雙對應點的直線都通過同一點O。
2.每雙對應點均在點O的同側(如圖1),或均在點O的異側(如圖2)。
3.對任一雙對應點A和A′,有OA′/OA=k,
則稱圖形F和F′位似,或稱圖形F位似於圖形F′,又稱圖形F和F′配景相似。圖形F和F′稱為位似圖形或位似形,點O稱為位似中心,對應點稱為位似點,定比k稱為“位似比”或位似係數,或位似率。當任一雙對應點A,A′在點O的同側,這時,圖形F和F′稱為順位似圖形,或稱圖形F和F′外位似,點O稱為外位似中心,或外相似中心。這時規定位似比k>0。當任一雙對應點A,A′在點O的兩側,這時圖形F和F′稱為逆位似,或稱圖形F和F′內位似,點O稱為內位似中心,或內相似中心。這時規定位似比k<0。位似圖形必為相似圖形,但反過來不一定成立。兩個位似圖形必為真正相似圖形。位似形是在位似變換下互相變換的圖形。
幾何變換
幾何變換是把一個幾何圖形按照某種法則或規律變成另一種圖形的過程。因為幾何圖形都是點的集合,所以幾何變換都是通過點的變換實現的。例如,在平面幾何中,作一個圖形關於某一條直線對稱的過程,就是一個幾何變換,它把一個圖形變成與原圖形對稱的圖形。這個變換稱為平面的反射變換。
把“幾何”與“變換”聯繫起來,為用近代數學方法討論幾何問題開闢了廣闊的前景.因此促進了幾何學的發展。而且幾何變換本身在繪圖、力學、機械結構的設計、航空攝影測量、電路網路等方面都有廣泛的套用。同時,由於幾何變換體現了一種運動變化的思想,而在數學數育中培養學生運動變化的觀點是一項重要內容,因此現代各國在中國小數學教學內容改革中,都注意增加幾何變換的內容,或滲透幾何變換的思想。
中學數學教學內容中涉及的幾何變換,主要有契約變換(包括平移變換、旋轉變換、反射變換)和相似變換。立體幾何中的簡單多面體變形屬於拓撲變換。契約變換、相似變換、反演變換通常稱為初等幾何變換。在高等幾何里,還要研究射影變換、仿射變換等。
相似變換
平面(空間)到其自身的一個映射,如果對於任意兩點A,B及其象A’,B’,有A’B’=KAB(K>0)。把這個映射叫做平面(空間)的相似變換。當k=1時,相似變換就是契約變換。相似變換保持兩直線所成角的大小不變,並且不改變圖形的形狀而改變其大小,兩個相似的平面圖形,其面積之比等於它們的相似比的平方。位似變換是相似變換的特殊情形。對於平面到其自身的一個映射,如果存在定點S及常數K (K≠0),使得對於任意點M及其象M’滿足:①S,M,M’三點共線;②SM’=(K)SM,把這種映射稱為以S為位似垂中心,K為位似比的位似變換。當 K>0時,對應的兩點在位似中心的同側,稱為順位似,S稱為外位似中心;當K<0時,對應的兩點在位似中心的異側,稱為逆位似,S稱為內位似中心。
位似變換
一種幾何變換。設O為平面上一定點,若某變換把平面上任意一點A變為直線OA上一點A′,並且|OA′|=k|OA|,k≠0,則稱這種變換為平面到它自身的位似變換,O為位似中心,k為位似比或位似係數。當k>0時,點A和A′位於直線OA上點O的同側,稱這種位似變換為正向位似變換,或順位似變換,O為外位似中心;當k<0時,點A和A′在直線OA上點O的兩側,稱這種位似變換為反向位似變換,或逆位似變換,O為內位似中心。
當k=1時,位似變換為恆等變換,當k=-1時,位似變換為以O為中心,旋轉角為180°的旋轉變換或中心對稱變換。
若圖形M上各點經過位似變換後得圖形M′時,則稱圖形M位似於圖形M′,或圖形M與M′位似。當|k|>1時,圖形被放大,當|k|<1時,圖形被縮小。
位似變換是一種特殊位置的相似變換。
相似形
如果兩個邊數相同的多邊形的對應角都相等,對應邊都成比例,這兩個多邊形叫做相似多邊形。相似多邊形的對應邊的比叫做相似比或相似係數。相似比等於1的相似多邊形就是全等多邊形。平行於三角形的一邊並且和其他兩邊相交的直線,所截得的三角形和原三角形相似。平行於三角形一邊的直線和三角形其他兩邊的延長線相 交,所構成的三角形與原三角形相似。DE∥BC,則△ADE∽△ABC,FG∥BC,F、G分別是AB、AC延長線上的一點,則△ABC∽△AFG。如果一個三角形的兩個角和另一個三角形的兩個角分別相等,那么這兩個三角形相似。如果一個三角形的兩條邊和另一個三角形的兩條邊對應成比例,並且夾角相等那么這兩個三角形相似。如果一個三角形的3條邊與另一個三角形的3條邊對應成比例,則這兩個三角形相似。如果兩個直角三角形有一個銳角相等,那么這兩個直角三角形相似。如果一個直角三角形的斜邊和一條直角邊與另一個直角三角形的斜邊和一條直角邊對應成比例,那么這兩個直角三角形相似。相似三角形的對應高的比,對應角平分線的比,對應中線的比都等於它們的相似比。相似多邊形的周長的比等於它們的相似比,相似多邊形的面積比等於它們相似比的平方。
