基本內容
位似圖形:如果兩個相似圖形的每組對應頂點所在的直線都交於一點,對應邊互相平行,那么這樣的兩個圖形叫做位似圖形。
位似中心:兩個位似圖形中每組對應頂點所在的直線都交於一點,這個交點叫做位似中心。
位似比:新圖形與原圖形的對應邊的長度之比。即位似圖形的相似比。
兩個三角形對應頂點的連線相交於一點且到各對應點成比例的兩個相似三角形,且兩個三角形的各邊分別平行,這樣的兩個三角形即為位似三角形。
條件
1.兩個三角形相似;
2.兩個三角形每組對應點的連線在一點;
3.兩個三角形對應邊互相平行。
三條件缺一不可,否則不是位似三角形。
性質
相似三角形具有如下性質:
①對應角相等;
②對應邊、對應高、對應中線、對應角的平分線以及周長等,它們的比都等於相似比;
③面積的比等於相似比的平方。
位似三角形不僅具有相似三角形的所有性質,而且還有如下性質:
①任意一對對應點到位似中心的距離之比都等於相似比,這個相似比也可稱為位似比;
②對應線段互相平行。
畫圖步驟
1.確定位似中心;
2.分別連線並延長位似中心和能代表原圖的關鍵點;
3.根據相似比,確定能代表所作的位似三角形的關鍵點;
4.順次連線上述各點,得到放大或縮小的圖形。
相關計算
例1.△ABC三個頂點坐標分別為A(2,-2),B(4,-5),C(5,-2),以原點O為位似中心,將這個三角形放大為原來的2倍。
解:在平面直角坐標系中,如果位似變換是以原點為位似中心,相似比為k,那么位似圖形對應點的坐標的比等於k或-k。所以對應點的坐標為A′(4 ,-4),B ′ (8,-10),C ′(10,-4)或A" (-4,4)B" (-8,10),C" (-10,4)。如圖1所示。
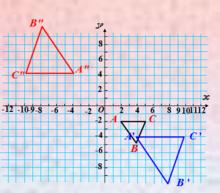 圖1
圖1套用教學
在位似三角形的數學教學中可以採用“探究法”。“探究法”的精髓在於以學生為主角,使他們由被動地接受知識轉變為知識的探索者。通過親自動手,積極思考,熱烈討論,探索知識,學生能更加深入理解知識的內涵,並培養觀察力、思維能力、動手能力、歸納能力、語言表達能力和創造能力等。“探究式教學法 ”是指在老師的指導下 ,學生通過具體的操作,親自嘗試後,經過積極思考和討論,找到知識的規律,總結出結論,學會新知,並發展思維、培養能力的綜合教學方法。通過讓學生對位似圖形進行進一步了解,可以引導學生對位似圖形中的位似三角形進行積極思考,從而使學生從本質上了解位似三角形的基本內容,最終明確兩個相似三角形的每組對應頂點所在的直線都交於一點,對應邊互相平行的兩個三角形為位似三角形這一概念,從中拓展學生思維、提高學生獨立思考的能力。

