定義
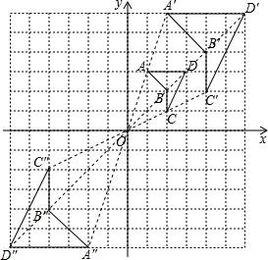
已知兩個幾何圖形A和A',若二者之間存在一個一一對應,且每一雙對應點P和P'都與一定點O共線,同時OP/OP'=k(k>0是常數),則稱A和A'位似,而點O叫做位似中心,k是位似比 。
位似圖形一定是相似圖形,相似圖形不一定是位似圖形。
特別地,兩個不重合的圓總是位似的,位似中心為兩圓外公切線或內公切線的交點。
性質
 位似
位似位似是特殊的相似。位似圖形對應邊平行,對應點的連線交於一點,這一點是位似中心。
位似圖形的對應幾何性質完全相同。
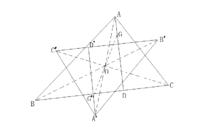
例如,已知△ABC與△A'B'C'位似,點O是位似中心。
設G為△ABC的垂心,GO的延長線交B'C'上的高線A'D'於點G',
那么G'就是△A'B'C'的垂心。
中心落點
位似圖形的中心可以在任意的一點,不過位似圖形也會隨著位似中心的位變而位變。
根據一個位似中心可以作兩個關於已知圖形一定位似比的位似圖形,這兩個圖形分布在位似中心的兩側,並且關於位似中心對稱。
注意
1、位似是一種具有位置關係的相似,所以兩個圖形是位似圖形,必定是相似圖形,而相似圖形不一定是位似圖形;
2、兩個位似圖形的位似中心有一個或兩個(偶數邊正多邊形時,比如兩個正方形如果位似,則有兩個位似中心。);
3、兩個位似圖形可能位於位似中心的兩側,也可能位於位似中心的一側;
4、位似比就是相似比.利用位似圖形的定義可判斷兩個圖形是否位似;
5、平行於三角形一邊的直線和其它兩邊相交,所構成的三角形與原三角形位似。
作圖步驟
利用位似變換可把一個圖形放大或縮小,若位似比大於1,則通過位似變換把原圖形放大,若小於1,則通過位似變換把原圖形縮小。
位似比,即位似圖形的相似比,指的是要求畫的新圖形與參照的原圖形的相似比
①首先確定位似中心,位似中心的位置可隨意選擇(除非題目指明);
②確定原圖形的關鍵點,如四邊形有四個關鍵點,即它的四個頂點;
③確定位似比,根據位似比的取值,可以判斷是將一個圖形放大還是縮小;
④符合要求的圖形不唯一,因為所作的圖形與所確定的位似中心的位置有關,並且同一個位似中心的兩側各有一個符合要求的圖形,最好做兩個。( 考試的時候看題目要求,如果同向位似,則向圖形同側做位似圖形,如果反向位似,則向圖形另一側做位似圖形。如果題目沒有要求,則根據方格紙給的格數來看,一般哪一側格子夠畫就畫在哪一側)
位似變換
把一個幾何圖形變換成與之位似的圖形,叫做位似變換。物理中的透鏡成像就是一種位似變換,位似中心為光心. 位似變換套用極為廣泛,特別是可以證明三點共線等問題.