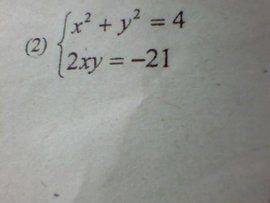示例
解:2x+y²+3xy+6x+2y+12=0…①,
且x²+4y²+4xy+x+y+15=0…②.
提示: 解方程的基本思想是消元與降次。僅僅就其消元而言，任給的①,②都難以直接用一個變數表示另一個變數(即用關於x的代數式表示y,或y的代數式用表示x)，其癥結在於二元二次項3xy,4xy，因此，首先需消去二元二次項。②*3-①*4，得到一個新的方程。再運用配方法分別將其x,y配方為如下形式:a(x+i)²+b(y+j)²+c=0,就可實現了用一個變數表示另一個變數，但其涉及到開方，且變為無理方程作解，比較複雜。就其降次而言，可運用因式分解法(包括十字相乘法的推廣:叉乘法及叉陣)，難度較大。也可以運用函式的解析法。在此，謹作點撥。總的而言，一般有三種普遍的方法：代數方程解法，因式分解法，運用函式。
求解
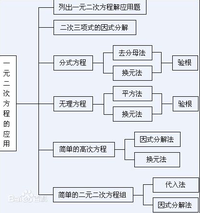二元二次方程二元二次方程組求解的基本思想是“轉化”，即通過“降次”、“消元”，將方程組轉化為一元二次方程或二元一次方程組。由於這類方程組形式龐雜，解題方法靈活多樣，具有較強的技巧性，因而在解這類方程組時，要認真分析題中各個方程的結構特徵，選擇較恰當的方法。
（1）有兩組相等的實數解。
（2）有兩組不相等的實數解；
（3）沒有實數解。解：將②代入①，整理得二次方程③的判別式
（4）當a<2時，方程③有兩個不相等的實數根，則原方程有不同的兩組實數解。
（5）當a=2時，方程③有兩個相等的實數根，則原方程有相同的兩組實數解。
（6）當a>2時，方程③沒有實數根，因而原方程沒有實數解。
