定義與一般形式
在初等代數中，二元二次方程組的定義為：由兩個未知數的一個二次方程和一個次數不超過二次的方程所組成的方程組。
二元二次方程組可分成兩種類型，第一類型是由一個二次方程和一個一次方程所組成的方程組，它的一般形式可寫成：
其中a，b，c不全為零，d和e也不全為零。第二類型是由兩個二次方程所組成的方程組，它的一般形式可寫成：
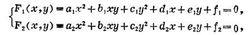二元二次方程組其中a，b，c不全為零，d和e也不全為零。
求解方法
對於上述第一類型的二元二次方程組，可用代入消元法，從而歸結為解含一個未知數的一個二次方程；而對於第二類型的二元二次方程組，經過消元後一般將歸結為一元四次方程，但對如下幾種特殊情形還是可以用一次和二次方程的方法來求解的：
1.存在數m和n，使mF(x，y)+nF(x，y)是一元方程；或是一次方程；或是可約。
2.F(x，y)和F(x，y)均為對稱多項式或反對稱多項式。
二元二次方程組最多可能有四組解。用代入法解二元二次方程組計算量大，計算困難（尤其是解無理方程和一元四次方程），因此必須尋找更簡便的方法。
特殊形式
二元二次方程組中有許多特例，例如：
A 有一個一次方程的二元二次方程組
B 對稱方程組
C 輪換方程組
D 不含一次項
E 二次項係數成比例
具體如下：
一個一次方程的二元二次方程組：
由一個二元一次方程和一個二元二次方程組成的方程組，一般用代入法求解，即將方程組中的二元一次方程用含有一個未知數的代數式表示另一個未知數，然後代入二元二次方程中，從而化“二元”為“一元”，如此便得到一個一元二次方程。此時，方程組解的情況由此一元二次方程根的情況確定。
例 解方程組：
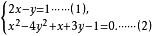二元二次方程組解：由(1)，得
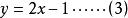二元二次方程組把(3)代入(2)，得
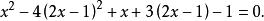二元二次方程組整理，得
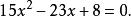二元二次方程組解這個方程，得
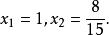二元二次方程組 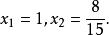二元二次方程組
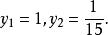二元二次方程組把 代入(3)，得
∴原方程上的解是：
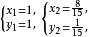二元二次方程組不含一次項：
不含有一次項的二元二次方程。通常解法為：嘗試將常數項通過加減消元消去。
例 解方程組
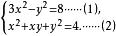二元二次方程組解：經觀察我們發現兩個方程都沒有一次項，則可以消去常數項，並分解因式。由①-②×2得：
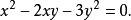二元二次方程組即
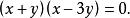二元二次方程組則原方程組與下列兩個方程組同解：
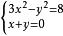二元二次方程組
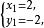二元二次方程組
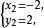二元二次方程組（1） ，解得 ， ；
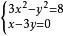二元二次方程組
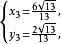二元二次方程組
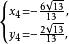二元二次方程組（2） ，解得 ， ；
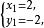二元二次方程組 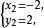二元二次方程組 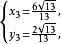二元二次方程組 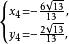二元二次方程組所以原方程的解為： ； ； ； ；
二次項係數成比例：
通常解法為：通過加減消元消除二次項
例 解方程組
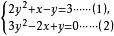二元二次方程組解：①×3-②×2得
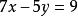二元二次方程組則原方程與下列方程組同解
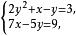二元二次方程組
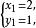二元二次方程組
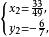二元二次方程組用代入法可得這個方程組（也即原方程組的解）： ；
對稱方程組：
將方程組中各方程的未知數互換後與原方程一樣，則此方程組為對稱方程組。解的特性：兩個未知數可以互換。
輪換方程組：
將方程組中各方程的未知數互換後，各方程變化，但是整個方程組不變。一般來說，將兩式相減即可因式分解。
