基本定義
 節點電壓法
節點電壓法對多支路兩節點電路的計算尤為簡便。
節點電壓是指電路中任一點到參考點之間的電壓。
參考點人為選擇.常以接地點為參考點。
求解方法
第一步:把電壓源與阻抗的串聯形式化為電流源與阻抗的並聯形式
第二步:標出節點,並把其中一個節點選為參考節點(一般為0電位點)
第三步:列出節點電壓方程。
列方程方法:自導納乘以該節點電壓+∑與該節點相鄰的互導納乘以相鄰節點的電壓=流入該節點的電流源的電流-流出該節點電流源的電流
註:這裡的“+”是考慮了互導納是導納的相反數,如果不考慮相反數的話,這個“+”就得寫為“-”
第四步:聯立求解出上面所有的節點電壓方程。
介紹
以節點電壓為求解對象的電路計算方法。節點電壓是在為電路任選一個節點作為參考點(此點通常編號為“0”),並令其電位為零後,其餘節點對該參考點的電位。一個支路數為b、節點數為n的電路,其節點電壓數為n-1,所以用節點電壓法計算時需要列出(n-1)個以節點電壓為未知量的獨立方程。
節點方程
 節點電壓法
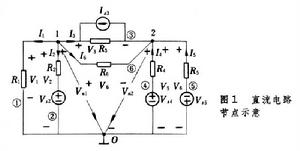
節點電壓法將KVL方程代入支路方程,消去支路電壓,再將所得新的支路方程,即支路電流與節點電壓的關係式代入KCL方程,消去支路電流後可得方程組此方程組的2個方程就是用節點電壓法計算圖1所示電路時需要列出的方程。這種方程通常稱為電路的節點方程。顯然,由節點方程可得出電路的2個節點電壓。將節點電壓代入KVL方程可求出電路的6個支路電壓,再將支路電壓代入支路方程(將節點電壓代入新的支路方程亦可),又能求出電路的6個支路電流。
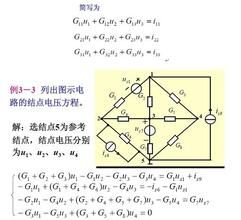
對照圖1可以發現,式(1)中Vn1的係數(G1+G2+G3+G6)是與節點“1”相連線的支路具有的電導之和,Vn2的係數-(G3+G6)是連線在節點“1”和節點“2”之間的支路具有的電導之和取負號;式(2)中的兩個係數類似。這4個係數可分別簡記為G11、G12、、。其中G11=G1+G2+G3+G6,稱為節點“1”的自電導;G12==-(G3+G6),稱為節點“1”與節點“2”間的互電導;=G3+G4+G5+G6,稱為節點“2”的自電導。還可發現,兩式右端項中的Is3是電流源的電流,因方向是指向節點“1”而取正號,背向節點“2”而取負號;另外幾項與電壓源有關的項是含電壓源的串聯支路變換成含電流源的並聯支路後,支路中電流源的電流,而且這些電流取正號或負號亦視方向是指向還是背向節點而定。同樣是指向者取正,背向者取負。例如式(1)中的就是圖1中支路2變換成如圖2所示支路中電流源的電流,余類推。節點電壓法
式(1)和式(2)可改寫成(3)式中的和分別是進入節點“1”和“2”的電流源電流之總和。
式(3)是3節點電路的通用節點方程,並可由它推出具有n個節點電路的通用節點方程式中左端項前的諸係數和右端項的含義以及正、負號的確定同前。式(4)可簡寫成(5)式中媠n是以自電導和互電導為元素的(n-1)×(n-1)矩陣,尓n是以節點電壓為分量的n-1維矢量,Is是以式(4)中的右端項為分量的n-1維矢量。
修改節點
當電路含有獨立電壓源構成的支路時,用此法會遇到困難。因為這種支路的方程是V=,無法用來在KCL方程中消去該支路的電流,所以事先應利用電源轉移的辦法(見電路變換)將此電壓源移走,然後再用此法計算。另外,電路若含有僅由壓控電壓源或流控電壓源或流控非線性元件構成的支路時,此法由於同上的原因而不能用。為了解決上述幾種支路給本法造成的困難,人們又創立了廣泛套用的修改的節點法。這個方法是將那些難以處理(對節點電壓法而言)的支路的電流也作為未知量引入節點方程內,同時再把它們的支路方程作為新方程引入節點方程組內形成獨立方程數與未知量數相等的新方程組。求解這一新方程組仍可求得全部節點電壓。
套用節點電壓法比支路電流法優越在於它需要直接求解的方程數少於後者。建立節點法所用方程的方法非常簡便。現今的電子計算機輔助電路分析程式,多是採用節點電壓法編制的。