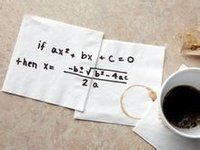整式方程
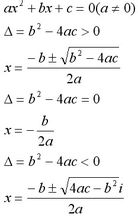二次方程二次方程是一種整式方程，其未知項的最高次數是2。
如果一個二次方程只含有一個未知數（x），那么就稱其為一元二次方程。
如果一個二次方程含有二個未知數（x和y），那么就稱其為二元二次方程，以此類推。
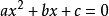二次方程二次方程中最常見的是一元二次方程。它的基本表達式為：
(a≠0）。其中a為方程的二次項係數，b為一次項係數，c為常數。若a = 0，則該方程沒有二次項，即變為一次方程。
一元二次方程的根
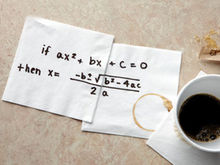二次方程的求根公式⑴若
，無實數根，有兩個複數根：x1=[-b+i√（4ac-b^2）]/（2a) ， x2=[-b-i√（4ac-b^2）]/（2a）；
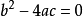二次方程⑵若
，有兩個相等實根：
；
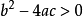二次方程⑶若
，有兩個不等實根：
,
。
二次方程公式可以歸納為如下形式：
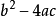二次方程其中
稱為根的判別式，常記為△。
推導過程：
移項，化二次項係數為1，得
x^2+b/ax=-c/a
兩邊同時加（b/（2a))^2，得
（x+b/（2a))^2=(b^2-4ac)/（4a^2）
x=[-b±√（b^2-4ac)]/（2a)
還可以令x=y-b/（2a），代入後消去一次項，得y^2=(b^2-4ac)/（4a^2），再減去b/（2a)
韋達定理
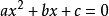二次方程對於一元二次方程
，有
，
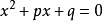二次方程特殊地，當二次項係數為1，即
時，
