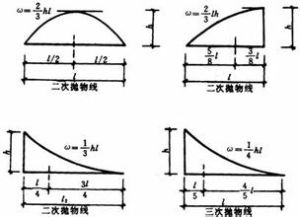
套用條件
(1)E * I = 常數C;
(2)桿軸為直線;
(3)影響線彎矩圖或實際荷載彎矩圖中有一個為直線圖形。
公式含義表示:
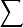 圖乘法
圖乘法位移Δ=彎矩圖面積ω*對應形心標距y/EI。
注意事項
(1) 必須符合上述前提條件;
(2)對應形心標距y只能取自直線圖形;
(3)彎矩圖面積ω與對應形心標距y若在桿件的同側則乘積取正號,異側則取負號。
套用舉例
 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法如圖所示,設等截面直桿AB段上的兩個彎矩圖中,圖為一段直線,而圖為任意形狀。我們以桿軸為X軸,以圖的延長線與X軸的交點O為原點並設定Y軸,則積分式中ds=dx,可提到積分號外面,為直線變化,故有,且常數,故上面的積分式成為
 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法式中,為圖中有陰影線的微分面積,故為微分面積對Y軸的靜矩。即為整個圖的面積對Y軸的靜矩,據合力矩定理,他應等於圖的面積乘以其形心C到Y軸的距離,即
 圖乘法
圖乘法代入上式有
 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法 圖乘法
圖乘法這裡是圖的形心C處所對應的圖的豎標。可見,上述積分式等於一個彎矩圖的面積乘以其形心處所對應的另一個直線圖形上的豎標,再除以EI,這就稱為圖乘法。