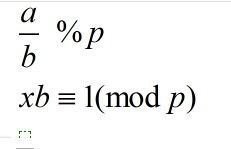定義
群G中任意一個元素a,都在G中有唯一的逆元a‘,具有性質aa'=a'a=e,其中e為群的單位元。
例
例如:4關於1模7的乘法逆元為多少?
4X≡1mod7
這個方程等價於求一個X和K,滿足
4X=7K+1
其中X和K都是整數。
若ax≡1modf,則稱a關於模f的乘法逆元為x。也可表示為ax≡1(modf)。
當a與f互素時,a關於模f的乘法逆元有解。如果不互素,則無解。如果f為素數,則從1到f-1的任意數都與f互素,即在1到f-1之間都恰好有一個關於模f的乘法逆元。
例如,求5關於模14的乘法逆元:
14=5* 2+4
5=4* 1+1
說明5與14互素,存在5關於14的乘法逆元。
1=5-4=5-(14-5* 2)=5* 3-14
因此,5關於模14的乘法逆元為3。
其求法可用歐幾里德算法:
ExtendedEuclid(d,f)//算法求d關於模f的乘法逆元d-1,即d* d-1 modf=1
1,(X1,X2,X3):=(1,0,f);(Y1,Y2,Y3):=(0,1,d)
2。if(Y3=0)thenreturnd-1 =null//無逆元
3。if(Y3=1)thenreturnd-1 =Y2//Y2為逆元
4。Q:=X3divY3//整除
5。(T1,T2,T3):=(X1-Q*Y1,X2-Q* Y2,X3-Q* Y3)
6。(X1,X2,X3):=(Y1,Y2,Y3)
7。(Y1,Y2,Y3):=(T1,T2,T3)
8。goto2
常用於加密算法中,如仿射算法。
代碼實現
//C++:inlinelonglongextend_gcd(longlonga,longlongb,longlong&x,longlong&y)
{
if(a==0&&b==0)
return-1ll;
if(b==0)
{
x=1ll;
y=0ll;
returna;
}
longlongd=extend_gcd(b,a%b,y,x);
y-=a/b*x;
returnd;
}
inlinelonglongmod_reverse(longlonga,longlongn)
{
longlongx,y,d=extend_gcd(a,n,x,y);
if(d==1)
return(x%n+n)%n;
else
return-1ll;
}