定義
角A的鄰邊比斜邊 叫做∠A的餘弦,記作cosA(由余弦英文cosine簡寫得來),即cosA=角A的鄰邊/斜邊(直角三角形)。記作cos=x/r。
餘弦是三角函式的一種。它的定義域是整個實數集,值域是[-1,1]。它是周期函式,其最小正周期為2π。在自變數為2kπ(k為整數)時,該函式有極大值1;在自變數為(2k+1)π時,該函式有極小值-1。餘弦函式是偶函式,其圖像關於y軸對稱。
定理
簡介
三角形任何一邊的平方等於其他兩邊平方的和減去這兩邊與它們夾角的餘弦的積的兩倍.
即
在餘弦定理中,令C=90°,這時cosC=0,所以
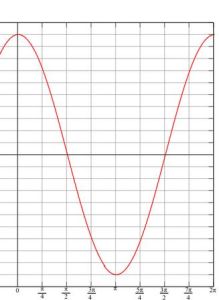
 餘弦.圖一
餘弦.圖一 餘弦.圖一
餘弦.圖一