共角定理

共角定理（外文名Common angle theorem）內容指的是若兩個三角形有一組對應角相等或互補,則它們的面積比等於對應兩邊乘積的比。別稱鳥頭模型、鳥頭定理。

基本信息

• 中文名稱：共角定理
• 外文名：Common angle theorem
• 別稱：鳥頭模型、鳥頭定理
• 套用學科：數學
• 適用領域範圍：數學

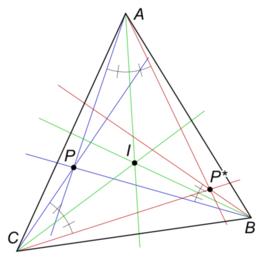
定理內容

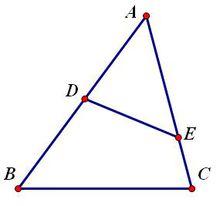共角定理

內容：若兩三角形有一組對應角相等或互補，則它們的面積比等於對應兩邊乘積的比。

即：若△ABC和△ADE中，

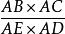共角定理

∠BAC=∠EAD ，則S△ABC÷S△AED=

推導過程

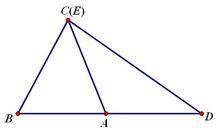共角定理

證明 ：

法一：

共角定理

由三角形面積公式S= ×a×b×sinC可推導出

S△ABC=1/2×AB×AC×sinA

S△ADE=1/2×AD×AE×sinA

∴S△ABC：S△ADE=AB×AC：AD×AE

證畢。

法二：

看到面積可作垂直做鋪墊。

共角定理

如右圖，分別過B、D點作AC垂線DF、BG交AC於點F、G。

則DF∥BG。

∴∠ADF=∠ABG

∵S△ABC：S△ADE=AC×BG：AE×DF

∠ADF=∠ABG

∴AD：AB=DF：BG

∴S△ABC：S△ADE=AB×AC：AD×AE。