經典力學,又稱古典力學或牛頓力學,是力學的一種,以三條牛頓運動定律作為基礎,在巨觀世界和低速狀態下
 經典力學
經典力學內容
經典力學的這三條定律是現代物理學的基礎,分別如下:
第一定律:如果物體處於靜止狀態或作勻速直線運動,只要沒有外力作用,物體將保持靜止狀態或勻速直線運動狀態。這也叫慣性定律;
第二定律:物體的加速度與所受的合外力成正比,與物體的質量成反比。加速度的方向與合力的方向相同。即a=\frac{F}{m};
第三定律:兩個物體的相互作用力總是大小相等,方向相反,同時出現或消失且作用於同一直線上。
經典力學的特點,是打破了絕對空間的概念,即在不同空間發生的事件是相對不同的,如運動車廂內靜止的物
 經典力學
經典力學由伽利略和牛頓等人發展起來的力學表述方式著重分析位移,速度,加速度,力等矢量間的關係,又稱為矢量力學,(有時牛頓力學這個辭彙也用來單指矢量力學)。它是工程和生活中最常用的,但並不是唯一的表述方式。拉格朗日(Lagrange)、哈密頓(Hamilton)、雅可比等發展了經典力學的新的表述形式,成為所謂分析力學(Analyticmechanics)。分析力學所建立的框架成為現代物理的基礎,如量子場論、廣義相對論、量子引力等。微分幾何的發展為它注入了新的生命力,成為現代經典力學的主要研究手段。
經典力學在日常經驗範圍內給出了精確的結果。現在,在接近光速的高速度或強大重力場的系統中,它被相對論力學取代;在小距離尺度系統中則被量子力學取代;在同時具有上述兩種特性的系統中被相對論量子場論取代。但是,經典力學仍然非常有用。因為:
它比上述理論簡單且易於套用。
 經典力學
經典力學它在很多場合近似正確。經典力學可用於描述人體尺寸物體的運動(例如陀螺(top)和棒球),很多天體(如行星和星系)的運動,以及一些微尺度物體(如有機分子)。
雖然經典力學和其他“經典”理論(如經典電磁學和熱力學)大致相容,在十九世紀末,還是有些只有現代物理才能解釋的不一致性被發現。特別的,經電非相對論電動力學預言光速相對於以太是常數,這一預測和經典力學無法調和,並導致了狹義相對論的發展。當和經典熱力學結合起來時,經典力學導出吉布斯佯謬(熵無定義)和紫外災難(黑體發射無窮能量)。為解決這些問題的努力導致了量子力學的發展。
簡介
力學在量子力學出現前的總稱,研究巨觀物體的運動規律,包括以牛頓運動定律為基礎的經典理論和狹義相對論。I.牛頓在1687年出版的《自然哲學的數學原理《一書中提出的運動三定律和萬有引力定律為經典力學奠定了基礎。L.歐拉、 J.-L.拉格朗日、W.R.哈密頓等繼牛頓之後,發展了不同的體系,推廣了力學在自然科學和工程技術中的套用。
學者們根據經典力學的定律和萬有引力定律曾經精確地預言彗星和小行星等的運動,並且得到了驗證;還根據這
 經典力學
經典力學以牛頓定律為基礎的力學理論是有它的局限性的。當物體的運動速度可與光速比擬時,對運動的分析要求放棄絕對空間和時間的概念,A.愛因斯坦於1905年建立的狹義相對論對此作了徹底的改革。在狹義相對論中,給出了長度收縮效應和時間膨脹效應,從而得出質點的質量是速度的函式,當質點速度接近光速時,質量趨於無限大。在物體的速度比光速小得多的條件下,牛頓定律成為相對論的特殊情況。在相對論動力學中也可套用拉格朗日和哈密頓的方法,但此時的拉格朗日函式和哈密頓函式不同於非相對論力學中的相應函式。
20世紀20年代,L.-V.德布羅意、E.薛丁格、W.K.海森伯、P.A.M.狄喇克等物理學家建立了研究電子、質子等微觀粒子行為的量子力學。量子力學的一個基本觀點是微觀粒子的行為不能以空間和時間的確定函式表達,故量子力學是非經典的。
由於牛頓力學和相對論力學在描述物體行為的觀點上是一致的,現代的經典力學著作都把狹義相對論的知識作為經典力學的組成部分。這些著作常包括牛頓力學和其重要發展體系──拉格朗日體系、哈密頓體系,以及狹義相對論等部分。因此,經典力學可分為非相對論經典力學和相對論經典力學。
理論的表述
經典力學有不同的理論表述方式:
1.牛頓力學(矢量力學)的表述方式。
2.拉格朗日力學的表述方式。
 經典力學
經典力學3.哈密頓力學的表述方式。
下面按照矢量力學的表述方式介紹經典力學的基本概念。為簡單起見,使用質點的概念,它是可以忽略大小的物體。質點運動可用一些參數描述:位置,質量,和作用在其上的力。
在現實中,經典力學可以描述的物體總是具有非零的尺寸。真正的點粒子,例如電子,用量子力學才能真正描述。非零尺寸的物體比虛構的點粒子有更複雜的行為,因為它們的內部結構可以改變-例如,棒球在移動的時候可以鏇轉。但是,點粒子的結果可以用於研究這種物體,因為可以把它們當成有大量點粒子組成的複合物體。這種複合物體和點粒子行為相似,如果他們小到和所研究的問題的距離尺度相比很小的話,因為這表示使用點粒子在這個問題內沒有矛盾。
位置及其導數
質點的位置是相對於空間的任意固定點定義的,固定點有時稱為原點,O。它定義為從O指向粒子的向量r。通常,質點不是靜止的,所以r是t(從任意的初始時刻開始的時間)的函式。在愛因斯坦之前的相對性理論
 經典力學
經典力學速度
速度,或者說位置的變化率,定義為位置對於時間的導數,也就是
\mathbf{v}={d\mathbf{r}\overdt}.
在經典力學中,速度是直接可加可減的。例如,如果一輛車以向東60km/h的速度超過一輛以50km/h向東的車,從被超的車上的人的角度來講,它的速度是向東60−50=10km/h.從快一點的車上的人的角度來看,慢一點的車以10km/h向西開。如果車是向北開呢?速度作為向量還是直接可加;但必須用向量分析的辦法來處理。
數學上,如果前面討論的第一個物體的速度用向量v=vd表示,第二個物體的速度用向量u=ue表示,其中v是第一個物體的速率,u是第二個物體的速率,而d和e分別是兩輛車運動方向上的單位向量,則第一個物體的速度從第二個物體來看,為
v'=v-u
類似的:
u'=u-v
當兩個物體在同一個方向運動,這個方程簡化為
 經典力學
經典力學v'=(v-u)d
或者,如果忽略方向,可以只用速率表達這個差
v'=v-u
加速度
加速度,或是說速度的變化量,是速度對於時間的導數或表示成
\mathbf{a}={d\mathbf{v}\overdt}.
加速度矢量可以改變大小、改變方向、或同時改變兩者。如果v的大小減小,有時意味著減速或變慢;但通常速度上的任何改變,包括減速,只是簡單的稱之為加速度。
參照系
下面的結果是關於同一個事件在兩個參照系S和S'的表述,其中S'以u為相對速度相
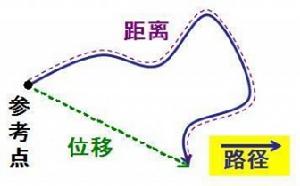 經典力學
經典力學v'=v-u(從S'來看,質點的速度比從S來看慢u)
a'=a(質點的加速度和參照系無關)
F'=F(因為F=ma)(質點上的力和參照系無關;見牛頓運動定律)
光速不是常數。
麥克斯韋方程組的形式不是獨立於參照系的。
力;牛頓第二定律
牛頓第二定律把質點的質量和速度同一個稱為力的向量聯繫
 經典力學
經典力學\mathbf{F}={d(m\mathbf{v})\overdt}.
量mv稱為動量.一般的,質量m是時間的常數,牛頓定律可以簡化為
\mathbf{F}=m\mathbf{a}
這裡a是加速,跟上面定義的一樣。但m並不總是獨立於t的。例如,火箭的質量在推進劑噴出的時候減少。在這種情況下,上面的方程式不正確,必須使用牛頓第二定律的完整形式。
牛頓第二定律不足以獨立表述粒子的運動。它需要知道F的值,這要通過考慮質點與之作用的特定物理實體來獲得。例如,一個典型的摩擦力可以用質點的速度的函式來表示,例如:
\mathbf{F}_{\rmR}=-\lambda\mathbf{v}
其中λ是一個正常數.一旦每個作用在質點上的力的獨立關係都給定了,它們可以代入到牛頓第二定律中來得到一個微分方程,稱為運動方程。繼續上面的例子,假設摩擦力是唯一作用在質點上的力.則運動方程為
-\lambda\mathbf{v}=m\mathbf{a}=m{d\mathbf{v}\overdt}.
 牛頓
牛頓這個可以積分,得到
\mathbf{v}=\mathbf{v}_0e^{-\lambdat/m}
其中v0是初速度。這表示這粒子的速度隨著時間指數式遞減到0。這個表達式可以進一步積分來得到位置r作為的時間的函式
重要的力包括重力和電磁學中的洛倫茲力。另外,牛頓第三定律有時可以用來簡化作用在質點上的力:如果已知粒子A作用力F在另一粒子B上,則B作用一個相等的但相反的反作用力,-F,到A上.
能量
若果力F作用到粒子上產生位移δr,該力做的功是一個標量
 經典力學
經典力學\deltaW=\mathbf{F}\cdot\delta\mathbf{r}.
若粒子的質量不變,而δWtotal是質點上所有的功,通過把每個力所作的功加起來得到,從牛頓第二定律有:
\deltaW_{\rmtotal}=\deltaT\,,
這裡T稱為動能.對於一個質點,它定義為
T={m|\mathbf{v}|^2\over2}.
對於很多粒子組成的複合物體,合成體的動能是粒子的動能總和.
對於稱為保守力的一類特殊的力,可以表達為一個標量函式的梯度,該函式稱為勢能記
 經典力學
經典力學\mathbf{F}=-\nablaV.
如果所有總用在粒子上的力是保守的,而V是通過把所有勢能加起來得到的總勢能,
\mathbf{F}\cdot\delta\mathbf{r}=-\nablaV\cdot\delta\mathbf{r}=-\DeltaV\,\!\RightArrow-\deltaV=\deltaT
\,\!\Rightarrow\delta(T+V)=0.
這個結果稱為能量守恆定律,表明總能量,E=T+V,是時間的常數。這常常很有用,因為很多常見的力是保守的。
進一步的結果
牛頓的定律為複合物體提供了很多重要的結果。見角動量(angularmomentum).
經典力學有兩個重要的表述:拉格朗日力學和哈密爾頓力學.它們都和牛頓力學等價,但是在解決問題是經常更有用。這些和其他的現代表述通常都繞過"力"的概念,而使用其他物理量,例如能量,來描述力學系統。
例子
考慮兩個參照系,其中一個以u的相對速度相對於另一個運動。例如,一輛車以10km/h的相度速率超過另一輛車,u就是10km/h.
兩個參照系SandS',其中S'以u的相對速度相對於S運動;一個事件在S中的時空坐標為(x,y,z,t)而在S'中為(x',y',z',t')。
 經典力學
經典力學在伽利略-牛頓相對性中的一個事件的時空坐標的變換由一套定義了稱為伽利略變換的群變換的公式來決定。
設時間在所有參照系中絕對,在相差一個x方向上的相對速度u的兩個坐標系(令x=ut當x'=0)中的時空坐標關係為:
x'=x-ut
y'=y
z'=z
t'=t
歷史
希臘人,特別是亞里士多德,是第一個提出有抽象的原則支配著自然的。
伽利略是最早給出抽象定律的科學家之一,他可能真的做了從比薩斜塔扔下兩個鉛球的著名的實驗。(理論和實踐表明他們同時落地)。雖然上面這個實驗的真實性受到懷疑,但他確實做了斜面上滾球的定量實驗;他關於加速運動的正確理論顯然是由這些結果導出的。
艾薩克·牛頓爵士是第一個給出三大定律(慣性定律,上面提到過的關於加速度的第二定律,和作用與反作用的定律)的人,並證明這些定律同時支配著日常生活中的物體和天體。
牛頓也發展了微積分,那對經典力學的數學計算是必須的。
牛頓之後,這個領域變得更數學且更抽象。
經典力學研究
經典力學研究InternationalJournalofMechanicsResearch是一本關注力學領域最新進展的國際中文期刊,由漢斯出版社發行。本刊支持思想創新、學術創新,倡導科學,繁榮學術,集學術性、思想性為一體,旨在為了給世界範圍內的科學家、學者、科研人員提供一個傳播、分享和討論力學領域內不同方向問題與發展的交流平台。
研究領域:
·經典力學
 經典力學研究
經典力學研究·基礎力學
·分析力學
·材料力學
·固體力學
·流體力學
·彈性力學
·板殼力學
·塑性力學
·斷裂力學
·結構力學
·套用力學
·工程力學
·流變學
·爆炸力學
·物理力學
·化學流體動力學
·電漿動力學
·電流體動力學
·磁流體力學
·熱彈性力學
力學其他學科
參考書目
H.Goldstein, Classical MechanicsAddison-Wesley,Reading,麻薩諸塞,1980年。
E.A.Desloge,ClassicalMechanicsSons,紐約1982年。
J.W.Leech,ClassicalMechanics,Mothuen,倫敦1958年。
H.C.Corbenand P.Stehle,經典力學,JohnWiley&Sons,紐約1960年

