定義
在分析力學裡，一個動力系統的 拉格朗日函式，是描述整個物理系統的動力狀態的函式，對於一般經典物理系統，通常定義為動能減去勢能，以方程表示為
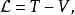拉格朗日函式
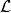拉格朗日函式
拉格朗日函式
拉格朗日函式其中， 為拉格朗日量， 為動能， 為勢能。
在分析力學裡，假設已知一個系統的拉格朗日函式，則可以將拉格朗日量直接代入拉格朗日方程，稍加運算，即可求得此系統的運動方程。
概念
拉格朗日函式 拉格朗日函式拉格朗日量是動能 與勢能 的差值：
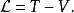拉格朗日函式
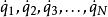拉格朗日函式
拉格朗日函式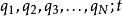
拉格朗日函式
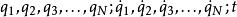拉格朗日函式通常，動能的參數為廣義速度 （符號上方的點號表示對於時間 的全導數），而勢能的參數為廣義坐標 ，所以，拉格朗日函式的參數為 。解析一個問題，最先要選擇一個合適的廣義坐標。然後，計算出其拉格朗日函式。假定這些參數（廣義坐標、廣義速度）都互相獨立，就可以用拉格朗日方程來求得系統的運動方程。
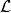拉格朗日函式假設一個物理系統的拉格朗日量為 ，則此物理系統的運動，以拉格朗日方程表示為
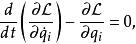拉格朗日函式 拉格朗日函式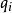
拉格朗日函式
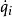拉格朗日函式其中， 是時間， 是廣義坐標， 是廣義速度 。
1.拉格朗日函式與作用量的關係
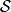拉格朗日函式一個物理系統的作用量 是一種泛函，以數學方程定義為
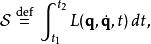拉格朗日函式
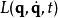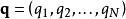拉格朗日函式
拉格朗日函式 拉格朗日函式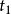
拉格朗日函式
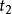拉格朗日函式其中， 是系統的拉格朗日量，廣義坐標 是時間 的函式， 和 分別為初始時間和終結時間。
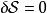拉格朗日函式 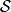拉格朗日函式
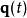拉格朗日函式假若，作用量的一次變分 ，作用量 為平穩值，則 正確地描述這物理系統的真實演化。從這變分運算，可以推導出拉格朗日方程 。
2.拉格朗日函式與能量守恆定律的關係
思考拉格朗日函式對於時間的全導數：
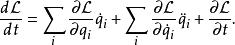拉格朗日函式將拉格朗日方程代入，可以得到
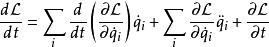拉格朗日函式
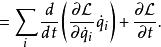拉格朗日函式
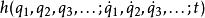拉格朗日函式定義能量函式 為
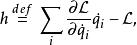拉格朗日函式則能量函式與 拉格朗日函式有以下含時關係式：
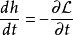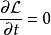拉格朗日函式
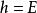拉格朗日函式
拉格朗日函式
拉格朗日函式假若拉格朗日量顯性地與時間無關， ，則能量函式是個常數： 。稱這常數 為這物理系統的能量。因此，這物理系統的能量守恆。
分析原理
分析力學方面
在分析力學裡，一個動力系統的拉格朗日量（英語：Lagrangian），又稱為拉格朗日函式，是描述整個物理系統的動力狀態的函式，對於一般經典物理系統，通常定義為動能減去勢能。
力學方面
在力學繫上只有保守力的作用，則力學系及其運動條件就完全可以用拉格朗日函式表示出來。這裡說的運動條件是指系統所受的主動力和約束。因此，給定了拉氏函式的明顯形式就等於給出了一個確定的力學系。拉氏函式是力學系的特性函式。
