簡史
亨德里克·安東·洛倫茲在物理學上最重要的貢獻是發展了經典電子論。1878年,他發表了光與物質相互作用的論文,把以太與普通的物質區別開來,認為以太是靜止的,無所不在,而普通物質的分子則都含有帶電的諧振子;在這個基礎上,他導出了分子折射率的公式(即洛倫茲-洛倫茨公式)。
l892年,他開始發表電子論的文章,他認為一切物質的分子都含有電子,電子是很小的有質量的剛球,電子對於以太是完全透明的,以太與物質的相互作用歸結為以太與物質中的電子的相互作用。
在這個基礎上,1895年他提出了著名的洛倫茲力公式。
另外,l892年他研究過地球穿過靜止以太所產生的效應,為了說明麥可遜-莫雷實驗的結果,他獨立地提出了長度收縮的假說,認為相對以太運動的物體,其運動方向上的長度縮短了。
1895,他發表了長度收縮公式。l899年,他討論了慣性系之間坐標和時間的變換問題,並得出電子質量與速度有關的結論。
1904年,他發表了著名的洛倫茲變換公式,以及質量與速度的關係式,並指出光速是物體相對於以太運動速度的極限。
從阿爾伯特·愛因斯坦狹義相對論的“相對性原理”和“光速不變原理”可推導出長度收縮效應,它顯示了空間性的相對性。長度收縮效應不但導致物體之間位置和方向的非確定性,還導致物體體積和密度等物理量的可變性。物體在其運動方向上發生長度收縮是相對論時空觀的必然結果,與物體的內部結構無關。所有相對於觀察者運動的物體,在其運動方向上都要發生同等程度的收縮。
圖片說明
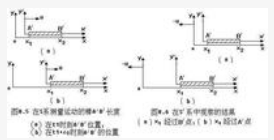
如圖所示,有兩個參考系S和S'。有一根棒A'B'固定在x'軸上,在S'系中測得它的長度為l'。為了求出它在S系中的長度l,我們假想在S系中某一時刻t1,B'端經過x1,在其後t1+Δt時刻A'經過x1。由於棒的運動速度為u。在t1+Δt這一時刻B'端的位置一定在x2=x1+uΔt處。根據上面所說長度測量的規定,在S系中棒長就應該是l=x2-x1=uΔt。現在再看Δt,它是B'端和A'端相繼通過x1點這兩個事件之間的時間間隔。由於x1是S系中一個固定地點,所以Δt是這兩個事件之間的原時。從S'系看來,棒是靜止的,由於S系向左運動,x1這一點相繼經過B'端和A'端(見圖8.6)。由於棒長為l',所以x1經過B'和A'這兩個事件之間的時間間隔Δt',在S'系中測量為Δt'=l'/u。現在再看Δt',它是不同地點先後發生的兩個事件的時間間隔,它是兩地時,根據原時和兩地時的關係,有Δt=Δt'√1-(v^2/c^2)=(l'/u)√1-(v^2/c^2)。將此式代入前式即可得l=l'√1-(v^2/c^2)。舉例說明
空間的量度與觀察這一量度的參照系有關。所以,在飛船上的尺和地球上的尺是不會一樣的。通過火車相對於月台的長度問題的討論,我們得知:沿運動方向固定在高速運動飛船上的尺,如果由地球上的人來觀測,就比飛船上的人觀測的長度短。至於長度收縮多少,是與飛船飛行的速度,也就是兩個參照系之間的相對速度有關。相反,固定在地球上的尺的長度,若由飛船上觀察者來觀測的話,則沿運動方向的長度不是伸長,也是縮短。由此,我們得出結論:當一個物體對於某參照系是靜止的時候,就這個參照系來看,物體長度最大。沿垂直於運動方向時,長度則不發生變化。這種長度收縮的現象是真實的嗎?這是不容懷疑的。不但運動的物體沿運動的方向產生收縮,而且收縮遵循著一定規律。這些都已從實際現象中得到證實。我們平時看不到這種收縮現象,是由於在低速緩慢的運動中,這種現象是不顯著的。例如,即使物體運動速度達到每秒3萬公里,長度的收縮也不過是千分之五。但是當物體運動速度接近光速時,情況就不同了,這時候長度的收縮非常顯著。靜止的時候,一米長的尺,沿相對運動方向的長度就會收縮成幾厘米。如果物體速度變得就等於光速,那么長度就會縮減成零。然而,這是不可能的。這一點也說明了光速是速度的最高限。一般物體的速度,無論如何也不會達到光速的。