由來
Irwin Sobel對於已經寫入數字圖像處理及機器視覺教科書多年的Sobel運算元，誰也沒曾追問和關心過它的發明背景和歷史。最近，給學生上“光電圖像處理”課，想介紹一下該運算元的來歷，查了很多文獻，就是找不到原始文獻。Google學術里搜尋，信息很多，卻不一致。有標註為期刊論文的，也有標註出版物析出的，出版時間也不一致（岡薩雷斯《Digital Image Processing》教材標註的時間為1970年）。
這個看似簡單，但領域內科研、開發人員沿用了幾十年的邊緣檢測運算元究竟如何產生的？偶然發現了一個帖子，該運算元的提出者Irwin Sobel在運算元產生多年後於該帖中詳細談到它的由來和定義。
原來，這個著名的Sobel邊緣運算元，當年作者並沒有公開發表過論文，僅僅是在一次博士生課題討論會(1968)上提出("A 3x3 Isotropic Gradient Operator for Image Processing")，後在1973年出版的一本專著（"Pattern Classification and Scene Analysis"）的腳註里作為注釋出現和公開的。
圖1 x和y兩個方向的sobel運算元模板
圖2 灰度圖像sobel運算元處理效果圖核心公式
該運算元包含兩組3x3的矩陣，分別為橫向及縱向，將之與圖像作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。如果以A代表原始圖像，Gx及Gy分別代表經橫向及縱向邊緣檢測的圖像，其公式如下:
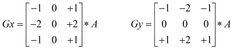Sobel運算元圖像的每一個像素的橫向及縱向梯度近似值可用以下的公式結合，來計算梯度的大小。
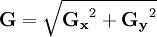Sobel運算元可用以下公式計算梯度方向。
Sobel運算元在以上例子中，如果以上的角度Θ等於零，即代表圖像該處擁有縱向邊緣，左方較右方暗。
運算元描述
在邊緣檢測中，常用的一種模板是Sobel 運算元。Sobel 運算元有兩個，一個是檢測水平邊緣的 ；另一個是檢測垂直邊緣的 。與Prewitt運算元相比，Sobel運算元對於像素的位置的影響做了加權，可以降低邊緣模糊程度，因此效果更好。
Sobel運算元另一種形式是各向同性Sobel(Isotropic Sobel)運算元，也有兩個，一個是檢測水平邊緣的 ，另一個是檢測垂直邊緣的 。各向同性Sobel運算元和普通Sobel運算元相比，它的位置加權係數更為準確，在檢測不同方向的邊沿時梯度的幅度一致。將Sobel運算元矩陣中的所有2改為根號2，就能得到各向同性Sobel的矩陣。
由於Sobel運算元是濾波運算元的形式，用於提取邊緣，可以利用快速卷積函式， 簡單有效，因此套用廣泛。美中不足的是，Sobel運算元並沒有將圖像的主體與背景嚴格地區分開來，換言之就是Sobel運算元沒有基於圖像灰度進行處理，由於Sobel運算元沒有嚴格地模擬人的視覺生理特徵，所以提取的圖像輪廓有時並不能令人滿意。 在觀測一幅圖像的時候，我們往往首先注意的是圖像與背景不同的部分，正是這個部分將主體突出顯示，基於該理論，我們給出了下面閾值化輪廓提取算法，該算法已在數學上證明當像素點滿足常態分配時所求解是最優的。
