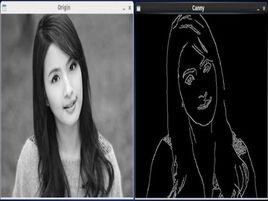
簡介
圖像的邊緣是圖像最基本也是最重要的特徵之一。邊緣檢測一直是計算機視覺和圖像處理領域的經典研究課題之一。圖像分析和理解的第一步常常是邊緣檢測。邊緣檢測的目的是去發現圖像中關於形狀和反射或透射比的信息，是圖像處理、圖像分析、模式識別、計算機視覺以及人類視覺的基本步驟之一。其結果的正確性和可靠性將直接影響到機器視覺系統對客觀世界的理解。
人類視覺系統認識目標的過程分為兩步：首先，把圖象邊緣與背景分離出來；然後，才能知覺到圖象的細節，辨認出圖象的輪廓。計算機視覺正是模仿人類視覺的這個過程。因此在檢測物體邊緣時，先對其輪廓點進行粗略檢測，然後通過連結規則把原來檢測到的輪廓點連線起來，同時也檢測和連線遺漏的邊界點及去除虛假的邊界點。
邊緣識別的實質是採用某種算法來提取出圖像中的對象與背景間的交界線。圖像灰度的變化情況可以用圖像灰度分布的梯度來反映，因此我們可以利用局部圖像微分技術獲得邊緣檢測運算元。
圖像邊緣
圖像的大部分信息都存在於圖像的邊緣中，主要表現為圖像局部特徵的不連續性，即圖像中灰度變化比較劇烈的地方。因此，我們把邊緣定義為圖像中灰度發生急劇變化的區域邊界。根據灰度變化的劇烈程度，通常將邊緣劃分為階躍狀和屋頂狀兩種類型。階躍邊緣兩邊的灰度值變化明顯，而屋頂邊緣位於灰度值增加與減少的交界處。那么，對階躍邊緣和屋頂邊緣分別求取一階、二階導數就可以表示邊緣點的變化。因此，對於一個階躍邊緣點，其灰度變化曲線的一階導數在該點達到極大值，二階導數在該點與零交叉；對於一個屋頂邊緣點，其灰度變化曲線的一階導數在該點與零交叉；二階導數在該點達到極大值。
邊緣識別步驟及要求
邊緣識別的步驟
邊緣識別主要包括以下四個步驟:
(1)圖像濾波
邊緣檢測算法主要是基於圖像亮度的一階和二階導數，但是導數的計算對噪聲很敏感，因此必須使用濾波器來改善與噪聲有關的邊緣檢測器的性能。
(2)圖形增強
增強邊緣的基礎是確定圖像各點鄰域強度的變化值。增強算法可以將鄰域強度值有顯著變化的點突出顯示。
(3)圖像檢測
在圖像中有許多點的梯度幅值比較大，而這些點在特定的套用領域中並不都是邊緣，應該用某些方法來確定那些是邊緣點。最簡單的邊緣檢測判據是梯度幅值閾值判據。
(4)圖像定位
如果某一套用場合要求確定邊緣位置，則邊緣的位置可以在子像素解析度上來估計，邊緣的方位也可以被估計出來。
邊緣識別要求
對於圖像的邊緣檢測來說，一般在識別過程中有如下的要求:
(1)首先能夠正確的檢測出有效的邊緣；
(2)邊緣定位的精度要高；
(3)檢測的回響最好是單像素的；
(4)對於不同尺度的邊緣都能有較好的回響並儘量減少漏檢；
(5)對噪聲應該不敏感；
(6)檢測的靈敏度受邊緣方向影回響該小。
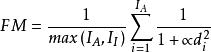邊緣識別這些要求往往都很矛盾，很難在一個邊緣檢測器中得到完全的統一。判斷邊緣檢測器性能的方法是先看邊緣圖像，再評價其性能，邊緣檢測器的回響中主要有三種誤差:丟失的有效邊緣、邊緣定位誤差和將噪聲誤判斷為邊緣。為了定量的評價邊緣檢測器的性能，1991年Pratt提出了一種綜合考慮上述三種因素的品質因數因素公式—Pratt品質因數
其中I，I，d，α分別是檢測到的邊緣、理想邊緣、實際邊緣與理想邊緣間的距離和用於懲罰錯誤邊緣的設計常數。但是由於包括了丟失的邊緣點、邊緣點的位置和錯誤的邊緣，因此，只能用於有限的幾種圖像。
傳統邊緣識別方法
邊緣識別的實質是採用某種算法來提取出圖像中的對象與背景間的交界線。圖像灰度的變化情況可以用圖像灰度分布的梯度來反映，因此我們可以利用局部圖像微分技術獲得邊緣檢測運算元。經典的邊緣檢測方法是對原始圖像中像素的某小鄰域來構造邊緣檢測運算元。
基於灰度直方圖
基於灰度直方圖門限法的邊緣檢測是一種最常用、最簡單的邊緣檢測方法。對檢測圖像中目標的邊緣效果很好。圖像在暗區的像素較多，而其他像素的灰度分布比較平坦。為了檢測出圖像物體的邊緣，把直方圖用門限T分割成兩個部分，然後對圖像f(i，j)實施以下操作:
(1)掃描圖像f(i，j)的每一行，將所掃描的行中每一個像素點的灰度與T比較後得g(i，j)；
(2)再掃描圖像f(i，j)的每一列，將所掃描的列中每一個像素點的灰度與T比較後得g(i，j)；
(3)將g(i，j)與g(i，j)合併，即得到物體的邊界圖像g(i，j)。
在以上過程中，門限T的選擇將直接影響邊緣檢測的質量。由於直方圖往往很粗糙，再加上噪聲的影響更是參差不齊。這樣就使得求圖像極大、極小值變得困難。因此，可以用兩條二次高斯曲線對目標和景物所對應的峰進行擬合，然後求二者的交點，並作為谷底，選取對應的灰度值為門限T，或用一條二次曲線擬合直方圖的谷底部分，門限T可取為T=-b/2a。
基於梯度
梯度對應一階導數，梯度運算元就是一階導數運算元。在邊緣灰度值過渡比較尖銳，且在圖像噪聲比較小時，梯度運算元工作的效果較好，而且對施加的運算方向不予考慮。對於一個連續圖像函式f(x，y)，其梯度可表示為一個矢量
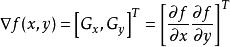邊緣識別這個矢量的幅度和方向角分別為
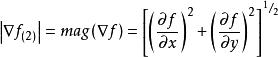邊緣識別以上各式的偏導數需對每個像素的位置計算，在實際中常用小區域模板進行卷積來近似計算。對G和G各用一個模板，將兩個結合起來就構成一個梯度運算元。根據模板的大小和元素值的不同，已提出許多不同的運算元，常見的有Roberts邊緣檢測運算元、Sobel邊緣檢測運算元、Prewitt邊緣檢測運算元、Robinson邊緣檢測運算元等.
1.Roberts邊緣運算元
Roberts邊緣檢測運算元是根據任意一對互相垂直方向上的差分可用來計算梯度的原理，採用對角線方向相鄰像素之差。Roberts邊緣檢測運算元採用對角線方向相鄰像素之差近似檢測邊緣，定位精度高，在水平和垂直方向效果較好，但對噪聲敏感。
2.Sobel邊緣檢測運算元
將圖像中的每個像素的上、下、左、右四鄰域的灰度值加權差，與之接近的鄰域的權最大。Sobel運算元利用像素的上、下、左、右鄰域的灰度加權算法，根據在邊緣點處達到極值這一原理進行邊緣檢測。該方法不但產生較好的檢測效果，而且對噪聲具有平滑作用，可以提供較為精確的邊緣方向信息。但是，在抗噪聲好的同時增加了計算量，而且也會檢測偽邊緣，定位精度不高。如果檢測中對精度的要求不高，該方法較為常見。
3.Prewitt邊緣運算元
Prewitt邊緣運算元是一種邊緣樣板運算元。樣板運算元由理想的邊緣子圖像構成，依次用邊緣樣板去檢測圖像，與被檢測區域最為相似的樣板給出最大值，用這個最大值作為運算元的輸出。
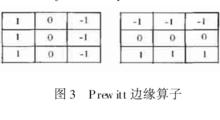Prew itt 邊緣運算元由圖所示的兩個卷積運算元形成了Prewitt邊緣運算元，與使用Sobel邊緣運算元的方法一樣，圖像中每個像素都用這兩個核做卷積，取最大值作為輸出，運算結果就是一幅邊緣圖像。適當取門限TH，如果R(i，j)≥TH則為階躍邊緣點。
Robinson邊緣運算元也是一種邊緣樣板運算元，其算法和Prewitt邊緣運算元相似，只是邊緣樣板不同。
4.Laplacan邊緣運算元
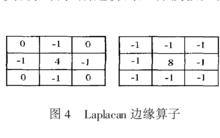Laplacan 邊緣運算元Laplacan運算元是二階微分運算元，它具有旋轉不變性，即各向同性的性質。數字圖像函式的拉普拉斯算法也是藉助各種模板卷積實現的。這裡對模板的基本要求是對應中心像素的係數應是正的，而對應中心像素臨近像素的係數應是負的，且所有係數的和應該是零，這樣不會產生灰度偏移，實現拉普拉斯運算的幾種模板見圖。
拉普拉斯邊緣運算元的缺點是:由於為二階差分，雙倍加強了噪聲的影響；另外它產生雙像素寬的邊緣，且不能提供邊緣方向的信息，因此，拉普拉斯運算元很少直接用於邊緣檢測，而主要用於已知邊緣像素，確定該像素是在圖像的暗區還是在明區。其優點是各向同性，不但可以檢測出絕大部分邊緣。
5.Canny邊緣檢測運算元
Canny運算元的基本思想是先將圖像使用高斯函式Gauss進行平滑，再由一階微分的極大值確定邊緣點。二階微分的零交叉點不僅對應著一階導數的極大值，而且也對應著一階導數的極小值。換句話說，圖像中灰度變化劇烈的點與變化緩慢的點都對應著二階導數零交叉點。因此，Canny運算元可能會引入偽邊緣點。
6.LOG濾波器
LOG濾波器又稱Marr-Hildreth模板或運算元。
即先對圖象平滑，後拉氏變換求二階微分，等效於把拉氏變化作用於平滑函式，得到1個兼有平滑和二階微分作用的模板，再與原來的圖象進行卷積。用Marr-Hildreth模板與圖象進行卷積的優點在於，模板可以預先算出，實際計算可以只進行卷積。
LOG濾波器有以下特點:
(1)通過圖象平滑，消除了一切尺度小於σ的圖象強度變化；
(2)若用其它微分法，需要計算不同方向的微分，而它無方向性，因此可以節省計算量；
(3)它定位精度高，邊緣連續性好，可以提取對比度較弱的邊緣點。
LOG濾波器也有它的缺點:當邊緣的寬度小於運算元寬度時，由於過零點的斜坡融合將會丟失細節。
幾種運算元的比較
Roberts運算元定位比較精確，但由於不包括平滑，所以對於噪聲比較敏感。Prewitt運算元和Sobel運算元都是一階的微分運算元，而前者是平均濾波，後者是加權平均濾波且檢測的圖象邊緣可能大於2個像素。這兩者對灰度漸變低噪聲的圖象有較好的檢測效果，但是對於混合多複雜噪聲的圖象，處理效果就不理想了。LOG濾波器方法通過檢測二階導數過零點來判斷邊緣點。LOG濾波器中的σ正比於低通濾波器的寬度，σ越大，平滑作用越顯著，去除噪聲越好，但圖象的細節也損失越大，邊緣精度也就越低。所以在邊緣定位精度和消除噪聲級間存在著矛盾，應該根據具體問題對噪聲水平和邊緣點定位精度要求適當選取σ。而且LOG方法沒有解決如何組織不同尺度濾波器輸出的邊緣圖為單一的、正確的邊緣圖的具體方法。Canny方法則以一階導數為基礎來判斷邊緣點。它是一階傳統微分中檢測階躍型邊緣效果最好的運算元之一。它比Roberts運算元、Sobel運算元和Prewitt運算元極小值算法的去噪能力都要強，但它也容易平滑掉一些邊緣信息。
