雙曲螺線的定義
在極坐標系中,極徑和極角成反比例的點的軌跡叫作 雙曲螺線( 倒數螺線) 。
雙曲螺線的方程
由雙曲螺線的定義可知,雙曲螺線的極坐標方程為
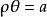 雙曲螺線
雙曲螺線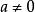 雙曲螺線
雙曲螺線(的常數).
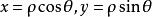 雙曲螺線
雙曲螺線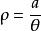 雙曲螺線
雙曲螺線以極點為原點,以極軸為橫軸的正半軸建立直角坐標系,由於,又由,這就得到直角坐標系中雙曲螺線的參數方程
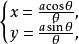 雙曲螺線
雙曲螺線 雙曲螺線
雙曲螺線(為參數).
雙曲螺線的基本性質
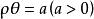 雙曲螺線
雙曲螺線雙曲螺線 的基本性質:
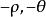 雙曲螺線
雙曲螺線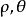 雙曲螺線
雙曲螺線(1) 對稱性 用代替方程中的,方程不變,所以雙曲螺線關於極垂線對稱。容易驗證,它關於極軸、極點都不對稱。
(2) 周期性 不存在。
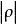 雙曲螺線
雙曲螺線(3) 存在範圍 因的值可以無窮大,所以曲線無限延伸。
 雙曲螺線
雙曲螺線 雙曲螺線
雙曲螺線 雙曲螺線
雙曲螺線 雙曲螺線
雙曲螺線(4) 漸近點與漸近線 當的絕對值由小趨向無窮大時,則的絕對值就逐漸減小而逐向於0,這就是說,雙曲螺線繞極點無限旋轉,雙曲螺線上的點與極點的距離趨近於0(這裡達不到0),所以極點是雙曲螺線的漸近點。如果的絕對值趨向於零,則的絕對就趨向無窮大,因此雙曲螺線向無窮遠延伸。另外
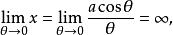 雙曲螺線
雙曲螺線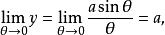 雙曲螺線
雙曲螺線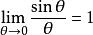 雙曲螺線
雙曲螺線(因).
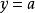 雙曲螺線
雙曲螺線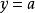 雙曲螺線
雙曲螺線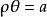 雙曲螺線
雙曲螺線這就是說,雙曲螺線上的點沿螺線向右或向左無窮遠離時,螺線上的點就無限地接近於直線,所以是雙曲螺線的一條漸近線 。
雙曲螺線的圖形
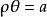 雙曲螺線
雙曲螺線雙曲螺線 的圖形:
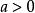 雙曲螺線
雙曲螺線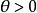 雙曲螺線
雙曲螺線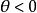 雙曲螺線
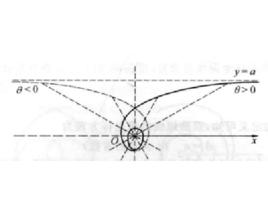
雙曲螺線(1)當時,用描點法先描出它的的部分,的部分可由它的對稱性描出(圖1)。
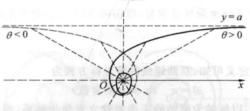 圖1
圖1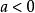 雙曲螺線
雙曲螺線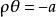 雙曲螺線
雙曲螺線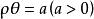 雙曲螺線
雙曲螺線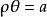 雙曲螺線
雙曲螺線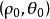 雙曲螺線
雙曲螺線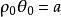 雙曲螺線
雙曲螺線(2)當常數時,這時的雙曲螺線也叫作 反雙曲螺線。反雙曲螺線與雙曲螺線關於極點對稱。這是因為,若M是上的任意一點,則M至少有一組坐標滿足這雙曲螺線的方程,即,由此就得
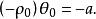 雙曲螺線
雙曲螺線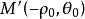 雙曲螺線
雙曲螺線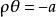 雙曲螺線
雙曲螺線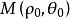 雙曲螺線
雙曲螺線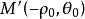 雙曲螺線
雙曲螺線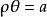 雙曲螺線
雙曲螺線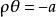 雙曲螺線
雙曲螺線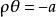 雙曲螺線
雙曲螺線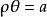 雙曲螺線
雙曲螺線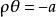 雙曲螺線
雙曲螺線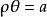 雙曲螺線
雙曲螺線這個等式說明是雙曲螺線上的一點,而和關於極點對稱。這就證明了上的每個點關於極點的對稱點必在上,反過來也成立,所以與關於極點對稱,與是全等的,只是它們在平面上與極軸的相關位置不同(圖2) 。
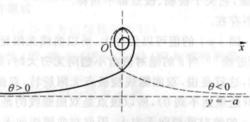 圖2
圖2