螺線
球面螺旋線螺線是切向量與一個固定的方向成定角的曲線。曲線為一般螺線的充分必要條件是它的撓率與曲率之比為常數，這類特殊曲線在力學工程技術中有著廣泛的套用。螺線可分為螺旋線(非平面曲線)及平面螺線。
在空間，一個動點M沿直線L作勻速直線運動，同時又以等角速度繞同平面的軸線Oz旋轉，M的軌跡是一條空間(非平面)曲線，稱為螺旋線。它分為左旋與右旋兩種。螺旋線是繞在圓柱面或圓錐面上的曲線，而它的切線與定直線(曲面的母線)的交角，是固定不變的。
對於平面螺線，是指在平面極坐標系中，如果極徑ρ隨極角θ的增加而成比例增加（或減少），這樣的動點所形成的軌跡。典型的螺線有球面螺旋線、阿基米德螺線、對數螺線、雙曲螺線等。
球面螺旋線
球面螺旋線
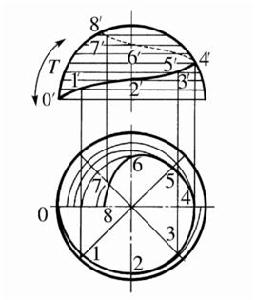
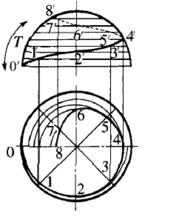
球面螺旋線球面螺旋線是一種常見的曲線，屬於螺旋線的一種。動點沿球面的子午線作等速圓弧運動，同時該子午線繞其軸線作等角速迴轉運動，動點的軌跡稱為球面螺旋線 。即一點沿著圓弧作等速度V的圓弧運動(經向運動)，而該圓弧又同時繞著中心軸(OZ軸)作等角速度 旋轉時，則該點的軌跡就是球面螺旋線。可見，這個螺旋線是以等速度V的圓弧運動和繞中心軸以等角速度。旋轉運動合成而得到的。
設xoy面為赤道面，由赤道面向上的球面螺旋線方程為：
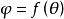球面螺旋線
球面螺旋線
球面螺旋線 球面螺旋線這裡取仰角 為自變數，方位角 中表示成 的函式。在球面上的半徑R是常數，則可寫出球面螺旋線的參數方程(直角坐標系)為 ：
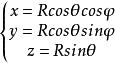球面螺旋線其他常見螺線
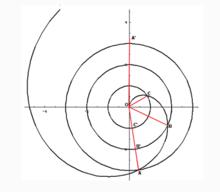
阿基米德螺線
阿基米德螺線是實踐中常用的一種曲線。動點在一直線上做勻速運動，而這條直線又圍繞著自己上面的一個定點作勻速轉動的動點的軌跡稱為阿基米德螺線，也叫等速螺線或平面螺線。它的極坐標方程為：
球面螺旋線
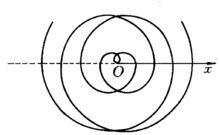圖1阿基米德在其《螺線》(On Spirals) 一書中引進了在極坐標ρ與θ之下的平面螺線ρ=aθ（如圖1所示），其繞線不在同一平面上。據說，阿基米德螺線最初是由阿基米德的老師柯農(歐幾里德的弟子)發現的。柯農死後，阿基米德繼續研究，又發現許多重要性質，因而這種螺線就以阿基米德的名字命名了。為解決用尼羅河水灌溉土地的難題，它發明了圓筒狀的螺旋揚水器，後人稱它為“阿基米德螺旋”。除了槓桿系統外，值得一提的還有舉重滑輪、灌地機、揚水機以及軍事上用的拋石機等。被稱作“阿基米德螺旋”的揚水機至今仍在埃及等地使用。一些噴淋冷卻塔所用的螺旋噴嘴噴出噴淋液的運動軌跡也為阿基米德螺線。
對數螺線
球面螺旋線
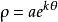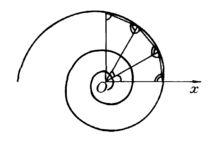
球面螺旋線對數螺線是一種特殊曲線。指在極坐標系中，極半徑ρ的對數與極角θ的比為常數的點M(ρ，θ)的軌跡。它的極坐標方程為 。式中，a、k為常數，e為自然對數的底。對數螺線上點M(ρ，θ)的切線與極半徑OM的夾角α都相等(cot α=k)，因而亦稱它為等角螺線。當極角按算術級數增加時，對數螺線的極半徑按幾何級數增加。對數螺線關於極點O的垂足曲線和反演圖形仍然是與原曲線全等的對數螺線，僅位置有所不同。對數螺線的漸伸線和漸屈線也都是對數螺線。對數螺線是1638年由笛卡兒(Descartes，R.)引入的，雅各布第一·伯努利(Bernoulli，Jacob Ⅰ)作了深入的研究，他在遺囑里吩咐要把對數螺線刻在他的墓碑上，因此又稱伯努利螺線。
從植物嫩枝的頂端往下，葉子大致上是按對數螺線排列的，這樣能使採光面積達到最大；在古生物的研究中，也套用了這種曲線。對數螺線上任一點的切線，與切點的矢徑相交成固定的角。這一性質在機械上有廣泛的套用。如果旋轉的切削刀沿此曲線的弧運動，就可保持固定的切削角，這種刀已在鋤草機中使用。為了製造的方便，對數螺線的短弧，可以用阿基米德螺線的短弧近似代替。
雙曲螺線
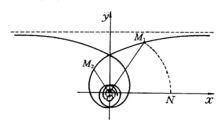球面螺旋線雙曲螺線，也稱反螺線，是一種特殊曲線，是阿基米德螺線關於極點的反演圖形。它是極徑和極角成反比例的動點軌跡。雙曲螺線的方程是：
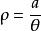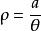球面螺旋線 球面螺旋線雙曲螺線以直線y=a為漸近線。曲線有兩支，它們關於y軸對稱。
