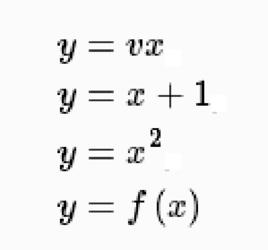定義
定義1
對於一個函式,如果已知自變數取某一值時,可以不必通過解方程即能求得因變數的對應值,這樣的函式叫做顯函式。 或者說若y是x的函式,當直接給出y等於一個只含自變數和中間變數的解析式子時,此時y叫做自變數x的顯函式。
參考定義2
 顯函式
顯函式 顯函式
顯函式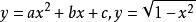 顯函式
顯函式顯函式:一個函式如果能用形如的解析式表示,其中分別是函式的自變數與因變數,則此函式稱為顯函式,如等都是顯函式。
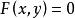 顯函式
顯函式 顯函式
顯函式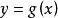 顯函式
顯函式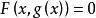 顯函式
顯函式隱函式:如果由方程可確定y是x的函式,即在某個範圍記憶體在函式,使,由這種方式表示的函式是隱函式。
參考定義3
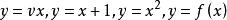 顯函式
顯函式顯函式:自變數與因變數已經明顯分離的函式稱為“顯函式”,如等都是顯函式。
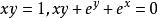 顯函式
顯函式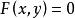 顯函式
顯函式隱函式:自變數與因變數沒有明顯分離或無法分離的函式稱為“隱函式”(意思是這種函式的函式關係“隱藏”在方程之中),如等都是隱函式,一元隱函式的一般形式是。
隱函式與顯函式的區別
如果方程f(x,y)=0能確定y與x的對應關係,那么稱這種表示方法表示的函式為隱函式。 隱函式不一定能寫為y=f(x)的形式,如x +y =0。因此按照函式"設x和y是兩個變數,D是實數集的某個子集,若對於D中的每個值,變數x按照一定的法則有一個確定的值y與之對應,稱變數y為變數x的(顯)函式,記作 y=f(x)"的定義,隱函式不一定是“函式”,而是“方程”。 也就是說,函式都是方程,但方程卻不一定是函式。顯函式是用y=f(x)表示的函式,左邊是一個y右邊是x的表達式 比如y=2x+1。隱函式是x和y都混在一起的,比如2x-y+1=0。有些隱函式可以表示成顯函式,叫做隱函式顯化,但也有些隱函式是不能顯化的,比如e +xy=1。
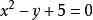 顯函式
顯函式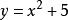 顯函式
顯函式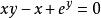 顯函式
顯函式顯函式與隱函式的區別不是絕對的。有些隱函式可以化成顯函式,如(R為常數)可以化成;有些隱函式如雖然也確定著x,y之間的函式關係,但y不能化為x的顯函式。
顯函式求導
 顯函式
顯函式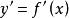 顯函式
顯函式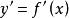 顯函式
顯函式 顯函式
顯函式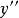 顯函式
顯函式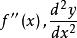 顯函式
顯函式若可導函式的導函式仍然可導,則稱的導數為函式的二階導數,記作,或,即
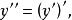 顯函式
顯函式或
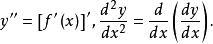 顯函式
顯函式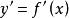 顯函式
顯函式 顯函式
顯函式相應地,稱為函式的一階導數。
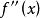 顯函式
顯函式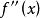 顯函式
顯函式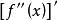 顯函式
顯函式 顯函式
顯函式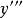 顯函式
顯函式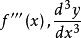 顯函式
顯函式類似地,若仍然可導,則稱的導數為函式的三階導數,記作,或。
 顯函式
顯函式 顯函式
顯函式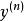 顯函式
顯函式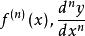 顯函式
顯函式一般地,若函式的n-1階導函式仍然可導,則稱n-1階導函式的導數為函式的n階導數,記作.或,即
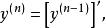 顯函式
顯函式或
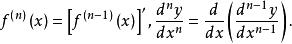 顯函式
顯函式 顯函式
顯函式 顯函式
顯函式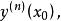 顯函式
顯函式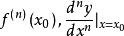 顯函式
顯函式函式在點處的n階導數值記作或。
 顯函式
顯函式 顯函式
顯函式函式的二階及二階以上的導數統稱為函式的高階導數。