定義
通常二重點是代數曲線上最簡單的奇點。
設C是代數曲線,P∈C是C上的奇點。
不妨設C在P附近的曲線方程 f(x,y)=0, 且P=(0,0)是原點。
P稱為二重點,如果f(x,y)的最低次項的次數是2;進一步,如果還要求C在P處恰好有兩條切線,就稱P是通常二重點。
局部方程
在適當的坐標變換下,通常二重點的局部方程可寫為標準方程: x -y =0。
設μ是C在P處的Milnor數,那么P是通常二重點若且唯若μ=1。
相關
代數曲線
在代數幾何中,一條 代數曲線是一維的代數簇。最典型的例子是射影平面P 上由一個齊次多項式f(X,Y)定義的零點。
奇點
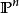 通常二重點
通常二重點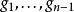 通常二重點
通常二重點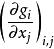 通常二重點
通常二重點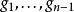 通常二重點
通常二重點曲線在一點P的平滑性可以用雅可比矩陣判斷。以下考慮嵌於中的曲線:設該曲線由n-1個n+1個變元的齊次多項式定義,若其雅可比矩陣在區線上一點P滿秩,則稱它P點光滑;反之則稱為奇點。在一點的平滑性與多項式的選取無關,也與曲線的嵌入方式無關。
在平面射影曲線的例子,假設曲線C由齊次方程式 f(x,y,z)=0定義,則C的奇點恰為C上使得f為零的點,即:
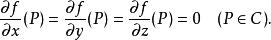 通常二重點
通常二重點在特徵非零的域上,一條代數曲線僅有有限個奇點;無奇點的曲線即 平滑曲線。奇點在雙有理映射下可能映為光滑點;事實上,奇點總是可借著平面的拉開映射或正規化解消,由此得到的新平滑曲線仍雙有理等價於原曲線;然而對代數封閉域上的射影曲線,其奇點總數則關係到曲線的幾何虧格,後者是個雙有理不變數。
