猶太民族在大家印象中是一個富於神秘色彩的民族, 國破家亡, 背井離鄉, 猶太人散落到世界各地. 固執的堅持自己的信仰, 自己的傳統, 生生不息, 代代相傳. 猶太名人眾多: 基督鼻祖耶穌, 共產主義之父馬克思, 科學泰斗愛因斯坦, 哲學大師弗洛伊德, 政壇名人基辛格等等. 不過也許大家不知道點集拓撲學的奠基人之一------豪斯道夫也是猶太后裔, 雖然他是一位知名數學家, 但他的猶太身份卻使他悲劇性的結束了自己的一生. 讓我們記住這位偉大的數學家!
簡介
Felix Hausdorff生平簡歷
Felix Hausdorff豪斯道夫在萊比錫學習數學，並在那裡任教，直至1910年獲聘往波昂任數學教授。納粹當權後，他想縱然自己是猶太人，但他是受敬重的大學教授，應可免於迫害。但他的抽象數學研究，竟然被批評為屬「猶太人」的，沒用而且「非德國」，令他在1935年失去教席。1942年，當他知悉終於避不過要被送往集中營，他與妻子和妻子的一名姊妹服毒自盡。
成就
豪斯多夫的興趣極為廣泛，不僅對數學、天文學和光學有興趣，而且也酷愛文學、哲學和藝術． 他的朋友主要是藝術家和作家．豪斯多夫曾用Dr．Paul Mongre的筆名出版了兩本詩集和一本哲學著作 (Das Chaos in Kosmischer Auslese， 1898)；還有大量的富有哲理的散文和文章．在1904年曾發表一部滑稽戲的劇本 (Der Arst Seiner Ehre)，這部戲在 1912年上演，獲得相當大的成功．他在1891—1896期間，曾發表過4篇天文學和光學的文章以及數學中許多分支的文章．1896年成為萊比錫大學講師，1902年成為副教授．以後主要致力於數學，逐漸減少了非科學的寫作，特別是1904年以後，主要研究集論．1910年，他作為副教授去波恩大學，在那裡寫出了著名的專題著作《集論基礎》(Grundzügeder Mengenlehre)，發表於1914年．這本專著影響極大，使豪斯多夫成為公認的一般拓撲學的奠基人．1913年，豪斯多夫在格賴夫斯瓦爾德(Greifswald)大學任教授．1921年回到波恩大學任教授，在波恩一直非常活躍，直到1935年，因為他是猶太人而被迫隱退．但他仍繼續從事集論和拓撲學的研究工作．他的成果只能在國外發表．1941年，他作為猶太人將被送到拘留營去．當拘留變得緊迫時，豪斯多夫和他的妻子、妻妹一起於1942年1月26日自殺于波恩．
豪斯多夫在數學的集合論、拓撲學、連續群理論、泛函分析、數論、機率論、幾何學等許多分支中都有建樹、最主要的貢獻是在集合論和點集拓撲學方面．
豪斯多夫將他的前輩導入的一些概念給予適當的概括，導入了許多新的觀念、方法和定理，發展為有系統的完美的理論，並為進一步發展提供了強大的動力．他是點集拓撲和度量空間的一般理論的創建者．
1906年，弗雷歇導入可數緊空間的概念，豪斯多夫於1914年給出了在豪斯多夫空間X中，X的任一無限子集有聚點為可數緊空間的特徵之一，並在度量空間中建立了序列緊性和可數緊性的等價性．他證明了任一可度量化空間X是第二可數的若且唯若X是可分的，以及緊可度量化空間是可分的．
關於連續擴張問題，豪斯多夫在1919年建立了：設A為可度量化空間X的閉子空間，則對X上的任一度量ρ，任一連續函式f：A→I確定X上f的連續擴張F為
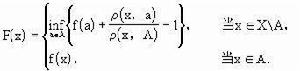費利克斯·豪斯道夫豪斯多夫《集論基礎》指出緊可度量化空間X到可度量化空間Y的任一連續映射f：X→Y關於空間X和Y上分別為ρ和σ的距離是一致連續的．
全有界空間的概念也是豪斯多夫《集論基礎》導入的，並在1927年證明了全有界度量空間是可分的[6]．
1914年，豪斯多夫證明了任一度量空間等距於某完備度量空間的子空間，刻畫了度量空間的完備化空間，證明了每個自稠密的完備度量空間含有子空間同胚於康托爾集，還證明了在所有完備可度量化空間中貝爾(Baire)綱定理成立．1927年又證明了完備化空間的唯一性．
Л．C．亞歷山德羅夫(AлeKcaHДpoЬ)對可分空間證明了完備度量化性關於Gδ集是可繼承的，豪斯多夫將此結果推廣於任意可度量化空間(1924)．
豪斯多夫和亞歷山德羅夫分別於1927和1925年獨立地證明了每個非空緊可度量化空間是康托爾集的連續象，即二進空間．這個結果對點集拓撲學的發展富有啟發意義．
設M是可度量化空間X的閉子空間，豪斯多夫於1930年證明了子空間M上的任一距離可擴張為空間X上的距離．
設f：M→L為可度量化空間X的閉子空間M到度量空間L上的連續映射，豪斯多夫證明了如果空間L可作為度量空間Y的閉子空間等距嵌入Y中[14]，則f可擴張為連續映射F：X→Y，使限制F|X＼M是X＼M到Y＼L上的同胚．
設2X為度量空間(X，ρ)的所有有界非空閉子集族，令
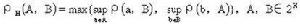費利克斯·豪斯道夫為A和B的距離，則(2X，ρh)為度量空間．稱ρh(A，B)為豪斯多夫距離(1914)．(X，ρ)等距於(2X，ρh)的閉子空間．但空間X上兩個等價的全有界距離ρ和σ，由ρh和σh在2X上導入的拓撲未必相同．豪斯多夫距離在度量空間的超空間理論中起著重要作用．
W．謝爾品斯基(Sierpinski)於1930年證明了若度量空間Y是可分完備可度量化空間X在開映射下的連續象，則Y是完備可度量化的．1934年，豪斯多夫證明了若可度量化空間Y是完備可度量化空間X在開映射下的連續象，則Y是完備可度量化的．以後E．麥克(Michael)又推廣於仿緊空間Y．
連通性的概念是M．E．C．若爾當(Jordan)於1893年研究平面的緊子集類時導入的．豪斯多夫推廣於抽象空間並開始了系統研究．在《集論基礎》中包含連通集的一些簡單性質，連通分支、擬分支的定義，以及關於緊度量空間的擬連通分支的性質等．該書還導入繼承不連通空間．
極不連通空間是M．H．斯通(Stone)在1937年定義的，但βN＼N不是極不連通的事實本身卻是由豪斯多夫證明的(1936)．
集X上的距離ρ稱為非阿基米德的，如果對所有x，y，z∈X，有
ρ(x，z)≤max[ρ(x，y)，ρ(y，z)]．
豪斯多夫證明了非空可度量化空間X，IndX=0若且唯若在空間X上存在非阿基米德距離(1934)．
在描述集合論方面，豪斯多夫《集論基礎》中研究了有序集的理論，如將序型分類，序型的有序積，有序集的表示等問題．他引入的極大原理可用來代替超限歸納法，是和選擇公理、良序原理、圖基(Tukey)引理、庫拉托夫斯基(Kuratowski)引理等命題等價的．
豪斯多夫提出的Rn中單位球分解(1914)，在空間轉動理論及變換群的分剖結果的基礎上，用選擇公理證明了使人感到奇怪的分球定理．以後導致S．巴拿赫(Banach)的分球悖論(1924)，即把一個球切成有限個片段，然後重新組合，可得到與原球有相同尺寸的兩個球．這一悖論使人懷疑選擇公理，引起數學界的極大重視，從而推進數學基礎的發展．
豪斯多夫還徹底解決了布萊爾集的基數定理(1916)，這是和亞歷山德羅夫同年獨立解決的．他還提出了豪斯多夫運算(1927)，豪斯多夫遞歸公式(1914)等．
1914年，豪斯多夫提出測度問題：是否存在Rn的每個子集均可測的有限可加測度？1923年，他證明了當n=1，2時存在無限多個解，當n≥3時無解．
在數學分析中，豪斯多夫從事矩量問題的研究並獲得重要結果，解決了有限區間的矩量問題及矩量的性質．他還得出了求和法及有關傅立葉係數的定理(1921)．
在連續群理論中，豪斯多夫建立了重要的代數算法，導出並研究了群論符號的指數公式(1906)．他也給出華林(Waring)問題的簡化證明(1909)並提出過任意非整維數(1919)．
豪斯多夫的工作對現代數學的形成和發展起著重要作用，以致現代數學中的某些術語是以豪斯多夫的名字命名的．如豪斯多夫公理、豪斯多夫空間、豪斯多夫距離、豪斯多夫一致空間、豪斯多夫拓撲群、豪斯多夫極大原理、豪斯多夫運算、豪斯多夫遞歸公式、豪斯多夫-楊(Young)定理等．
作品
中文名稱： 幾個特殊的自相似集的維數計算
論文編號： 3273996
英文名稱： The Calculation of Dimension of Several Special Self-Similar Sets
學位類型： 碩士畢業論文
專業： 套用數學
關鍵字： 豪斯道夫維數 盒維數 自相似集
