性質
(1)實數集的子集是連通的,若且唯若它是一個區間;
(2)連通性由同胚保持,從而是空間的拓撲性質;
(3)設Ω是X的一族子集,它們的並是整個空間X,每個Ω中的個體連通,且兩兩不分離(即任意兩個集合的閉包有非空交),則稱為‘X連通’;
(4)若X、Y連通,則乘積空間X×Y連通。
其他相關概念
連通空間
定義1:設X是一個拓撲空間。如果X中有兩個非空的隔離子集A和B,使得X= A∪ B,則稱X是一個不連通空間;否則,則稱X是一個連通空間。
局部連通空間
定義2:設X是一個拓撲空間。如果x∈ X的每一個鄰域中都包含著x的某一個連通的鄰域V,則稱拓撲空間在點x處是局部連通的。如果拓撲空間X在它的每一個點處都是局部連通的,則稱是一個局部連通空間 。
 連通性
連通性局部連通的拓撲空間也不必是連通的。例如,每一個離散空間都是局部連通空間,但包含著多於一個點的離散空間卻不是連通空間。又例如,n維歐氏空間 的任何一個開子空間都是局部連通的(這是因為每一個球形鄰域都同胚於整個歐氏空間,因而是連通的),特別地,歐氏空間本身是局部連通的。另一方面,歐氏空間中由兩個無交的非空開集的並作為子空間就一定不是連通的。
 連通性
連通性此外根據定義立即可見:拓撲空間X在點x X處是局部連通的若且唯若x的所有連通鄰域構成點二處的一個鄰域基。
道路連通空間
定義3:設X是一個拓撲空間,如果對於任何x, y,存在著X中的一條從x到y的道路(或曲線),我們則稱X是一個道路連通空間。X中的一個子集Y稱為X中的一個道路連通子集,如果它作為X的子空間是一個道路連通空間。
 連通性
連通性 連通性
連通性 連通性
連通性實數空間R是道路連通的,這是因為如果x, y R,則連續映射f: [0,1] R定義為對於任何t [0,1]有f(t)=x+t(y-x),便是R中的一條以x為起點以y為終點的道路。也容易驗證任何一個區間都是道路連通的 。
連通性問題
簡介
 圖1
圖1假設有個整數對,p-q解釋為p與q連通。如圖1所示。如果新輸入的對,可以由以前的輸入對連通,就不會輸出;如果不能由以前的對連通,就輸出這個對。例如2-9不在輸出之列,因為前面的對存在2-3-4-9的連通。
其可套用如下:
(1)整數代表網路節點,對代表網路連通,因此網路可以判斷p和q之間是否應經連通。
(2)電網。
(3)更甚至與程式中定義的兩個等價變數。
算法實現
首先假設連通的每個節點都存在一個數組中a[N],每次都選擇兩個節點,判斷兩個節點是不是連通。
(1)快速查找(quick-find)算法:程式如圖2所示,程式中若且唯若p與q連通的時候,id[p]與id[q]相等。
 圖2
圖2(2)快速並集算法:相比上面的算法,並集運算計算量少,查找運算計算量大,算是算法的改進。根本就是:每個節點都沿著樹上移,找到各自的根節點(root)。具體程式如圖3所示。
 圖3
圖3(3)快速並集的加權算法:
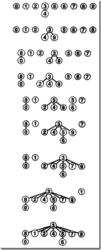 圖4
圖4上面的算法,我們並不能保證每一種情況,它的速度都比快速查找有實質性的提高。這個是修改版,它使用一個額外的數組sz完成維護的目的,為每個對象用id[i]==i來表示,這樣可以組織樹的增長。圖4描述了快速並集加權算法,連線兩棵樹的時候,較小的數的根要附屬到較大的數的根下面。這樣節點與根的距離短,多以查找效率要高。
如圖4所示,當處理1和6的時候,讓1、5、6都指向3,得到的樹比上面的算法更扁平。

