簡介
豪斯多夫距離是在度量空間中任意兩個集合之間定義的一種距離。
設 X和 Y是度量空間 M的兩個真子集，那么豪斯多夫距離 dH( X, Y)是最小的數 r使得 X的閉 r—鄰域包含 Y， Y的閉 r—鄰域也包含 X。
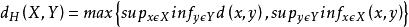豪斯多夫距離這距離函式令 M的所有真子集組成的集成為度量空間，且記為 F( M)。 F( M)的拓撲只是依賴於 M的拓撲。若 M是非空的，則 F( M)也是。
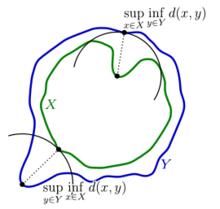圖1閉非真子集上的定義
豪斯多夫空間也可以照樣定義在 M的閉非真子集上，但距離可能是無限大， F( M)的拓撲不只依賴於 M的拓撲，也依賴於 M的特有度量。
非閉子集間的豪斯多夫距離可以定義為它們的閉包的豪斯多夫距離。這給予 M的所有子集組成的集一個偽度量。（兩個有相同閉包的子集的豪斯多夫距離是零）。
歐幾里得幾何上的定義
在歐幾里得幾何常用一個類似概念，稱為等距同構下的豪斯多夫距離。
設 X 和 Y是歐幾里得空間中兩個緊的圖形，則 DH( X, Y)是 dH( I( X), Y)取所有歐幾里得空間的保距變換 I的最小值。這距離量度 X和 Y離等距差多少。
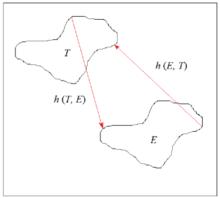圖2h(T,E) 表示了模板邊緣點與最近圖像邊緣點之間的最大距離；h (E,T) 的定義與h(T,E) 互為對稱，它表示了圖像邊緣點與最近模板邊緣點之間的最大距離。
Hausdorff距離是由這兩個距離的最大值決定。
