構造
去掉中心
1.取一個實心的三角形。（多數使用等邊三角形）
2.沿三邊中點的連線，將它分成四個小三角形。
3.去掉中間的那一個小三角形。
4.對其餘三個小三角形重複1。
取一個正方形或其他形狀開始，用類似的方法構作，形狀也會和謝爾賓斯基三角形相近。
Chaos Game
用隨機的方法（Chaos Game），都可得到謝爾賓斯基三角形：
任意取平面上三點A,B,C，組成一三角形
任意取三角形ABC內的一點P，畫出 該點
畫出 P和三角形其中一個頂點的中點
重複1
1.任意取平面上三點A,B,C，組成一三角形
2.任意取三角形ABC內的一點P，畫出 該點
3.畫出 P和三角形其中一個頂點的中點
4.重複1
L系統
下圖展示了曲線如何逼近謝爾賓斯基三角形。
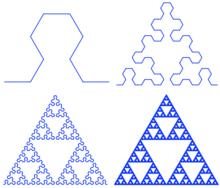圖1.曲線逼近這條曲線以L系統來記述為：
變數: A , B 常數: + , - 公理: A 規則: A → B-A-B B → A+B+A A,B ： 向前
- ： 左轉60°
+ ： 右轉60°
其他
先作一個正三角形，挖去一個“中心三角形”（即以原三角形各邊的中點為頂點的三角形），然後在剩下的小三角形中又挖去一個“中心三角形”，我們用黑色三角形代表挖去的面積，那么白三角形為剩下的面積（我們稱白三角形為謝爾賓斯基三角形）。如果用上面的方法無限連續地作下去，則謝爾賓斯基三角形的面積越趨近於零，而它的周長越趨近於無限大（如圖）。
若設操作次數為n（每挖去一次中心三角形算一次操作），則剩餘三角形面積公式為：4的n次方分之3的n次方。
將邊長為1的等邊三角形區域，均分成四個小等邊三角形，去掉中間一個，然後再對每個小等邊三角形進行相同的操作得……，這樣的操作不斷繼續下去直到無窮，最終所得的極限圖形稱為謝爾賓斯基墊片。謝爾賓斯基墊片的極限圖形的面積趨於零，而小圖形的數目趨於無窮，作為小圖形的邊的線段數目趨於無窮，實際上是一個線集。操作n次後邊長r=(1/2)n，三角形個數N(r)=3 n，根據公式N(r)=1/rD，3n=2Dr，D=ln3/ln2=1.585。所以謝爾賓斯基墊片是1.585。它比普通的一維直線占據了更多空間，但還是沒有二維正方形占據的那么多，可以用等比數列的知識求出他的面積是0。
