角平分線的定義
從一個角的頂點引出一條射線，把這個角分成兩個完全相同的角，這條射線叫做這個角的角平分線(bisectorofangle)。
三角形三個角平分線的交點叫做三角形的內心。三角形的內心到三邊的距離相等。
三角形的角平分線不是角的平分線：前者是線段，後者是射線。
其它解釋：角平分線可以看作是到角兩邊距離相等的所有點的集合。
其它解釋
三角形的一個角的平分線與這個角的對邊相交，連結這個角的頂點和交點的線段叫做 三角形的角平分線。（也叫三角形的內角平分線。） 由定義可知，三角形的角平分線是一條線段。 由於三角形有三個內角，所以三角形有三條角平分線。
角平分線角平分線的作法
在角AOB中，畫角平分線
2.分別以點M，N為圓心，以大於1/2MN的長度為半徑畫弧，兩弧交於點P。
3.作射線OP。
則射線OP為角AOB的角平分線。
當然，角平分線的作法有很多種。下面再提供一種尺規作圖的方法供參考。
作法：1.在兩邊OA、OB上分別截取OM、OA和ON、OB，且使得OM=ON，OA=OB；
2.連線AN與BM，他們相交於點P；
3.作射線OP。
則射線OP為角AOB的角平分線。
角平分線的性質
1.角平分線上的點，到這個角的兩邊的距離相等。
2.角平分線分得的兩個角相等，都等於該角的一半。3.角的內部到角的兩邊距離相等的點，都在這個角的平分線上。（逆運用）
角平分線定理
定理1
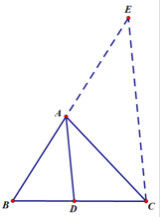
角平分線上的點到這個角兩邊的距離相等。證明：如圖，AD平分∠BAC，DB⊥AB，DC⊥AC
∵AD是∠BAC的平分線
定理1證明圖∴∠BAD=∠CAD
∵DB⊥AB，DC⊥AC
∴∠ABD=∠ACD=90°
又AD=AD
∴△ABD≌△ACD
∴CD=BD
故原命題得證。
該命題有逆定理：
在角的內部到一個角的兩邊距離相等的點在這個角的角平分線上。
證明：如圖，DB⊥AB，DC⊥AC，且DB=DC
∵DB⊥AB，
∴∠DBA=90
同理∴∠DCA=90
在RT△DBA和RT△DCA中，
{DB=DC(已知）
AD=AD（公共邊）
∴RT△DBA≌RT△DCA（HL）
∴∠BAD=∠CAD（全等三角形對應角相等）
定理2
三角形一個角的平分線分其對邊所成的兩條線段與這個角的兩邊對應成比例。證明：如圖2，在△ABC中，AD是∠BAC的平分線
過點D作DE⊥AB，DF⊥AC
∵AD是∠BAC的平分線，DE⊥AB，DF⊥AC
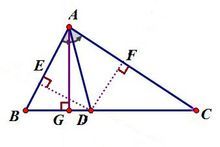定理2證明圖∴DE=DF(定理1)
∵2S△ABD=AB×DE,2S△ACD=AC×DF
∴S△ABD:S△ACD=AB:AC
過點A作AG⊥BC，,垂足為G
∵2S△ABD=BD×AG,2S△ACD=CD×AG
∴S△ABD:S△ACD=BD:CD
∴AB:AC=BD:CD
故原命題得證。
該命題有逆定理：
如果三角形一邊上的某個點分這條邊所成的兩條線段與這條邊的對角的兩邊對應成比例，那么該點與對角頂點的連線是三角形的一條角平分線。
證明略。
三角形的角平分線長
由定理2和斯台沃特定理可以推導出三角形內的角平分線長公式。如右圖，在△ABC中，AD平分∠BAC
可設AB=x,AC=y,BD=u,CD=v，則BC=u+v
由定理2我們知道AB:AC=BD:CD，所以xv=uy
由斯台沃特定理，有=(x²v+y²u)/(u+v)-uv
用u=xv/v,v=uy/x替換原式中的u和v
即得AD²=xy-uv=AB×AC-BD×DC
定理2的其它證明法
已知，如圖，AM為△ABC的角平分線，求證AB:AC=MB:MC面積法
由三角形面積公式，得S△ABM=(1/2)·AB·AM·sin∠BAM
面積法圖∵AM是∠BAC的角平分線
∴∠BAM=∠CAM
∴sin∠BAM=sin∠CAM
∴S△ABM:S△ACM=AB:AC
又△ABM和△ACM等高
設兩三角形的高為h
由三角形面積公式，得
S△ABM=(1/2)·BM·h
S△ACM=(1/2)·CM·h
∴S△ABM:S△ACM=BM:CM
∴AB:AC=MB:MC
相似法
過C作CN∥AB，交AM的延長線於N∵CN∥AB
相似法圖∴∠ABC=∠BCN
又∠AMB=∠CMN
∴△ABM∽△NCM
∴AB:NC=BM:CM
∵AM是∠BAC的角平分線
∴∠BAN=∠CAN
又∠BAN=∠ANC
∴∠CAN=∠ANC
∴AC=CN
∴AB:AC=MB:MC
（過M作MN∥AB交AC於N也可證明）
正弦定理法
作△ABC的外接圓，AM交圓於D由正弦定理，得
正弦定理法圖AB:sin∠AMB=MB:sin∠BAM,
AC:sin∠AMC=MC:sin∠CAM
∵AM是∠BAC的角平分線
∴∠BAM=∠CAM
又∠AMB+∠AMC=180°
∴sin∠BAM=sin∠CAM
sin∠AMB=sin∠AMC
∴AB:AC=MB:MC
性質套用舉例
三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。
如圖，若AD是△ABC的角平分線，則BD/DC=AB/AC。
證明：作CE∥AD交BA延長線於E。
∵CE∥AD
∴△BDA∽△BCE
∴BA/BE=BD/BC
∴BA/AE=BD/DC
∵CE∥AD
∴∠BAD=∠E,∠DAC=∠ACE
∵AD平分∠BAC
∴∠BAD=∠CAD
∴∠BAD=∠CAD=∠ACE=∠E
角平分線即∠ACE=∠E
∴AE=AC
又∵BA/AE=BD/DC
∴BA/AC=BD/DC
（註：例題中∵、∴分別表示為因為、所以）
判斷
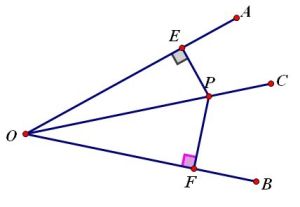
角的內部到角的兩邊距離相等的點，都在這個角的平分線上。判定定理的證明：如圖，已知PD⊥OA於D，PE⊥OB於E，且PD=PE，求證：OC平分∠AOB
證明：在Rt△OPD和Rt△OPE中：
OP=OP，PD=PE
∴Rt△OPD≌Rt△OPE（HL）
∴∠1=∠2
∴OC平分∠AOB
