角的平分線
定義:從一個角的頂點出發,把這個角分成兩個相等的角的射線,叫做這個角的平分線。(angular bisector)。
性質:角平分線上的點到角兩邊的距離(垂線段的長度)相等。
三角形頂點到其內角的角平分線交對邊的點連的一條線段,叫三角形的角平分線。
三角形的三條角平分線相交於一點,此點稱為三角形的內心,三角形的內心到三條邊的距離相等,是三角形內切圓的圓心。
三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。
三角形的角平分線上的點到角兩邊的距離(垂線段的長度)相等。
角的平分線的作法
在角AOB中,畫角平分線
作法:1.以點O為圓心,以任意長為半徑畫弧,兩弧交角AOB兩邊於點M,N。
2.分別以點M,N為圓心,以大於1/2MN的長度為半徑畫弧,兩弧交於點P。
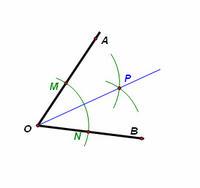 角的平分線
角的平分線3.作射線OP。
則射線OP為角AOB的角平分線。
當然,角平分線的作法有很多種。下面再提供一種尺規作圖的方法供參考。
作法:1.在兩邊OA、OB上分別截取OM、OA和ON、OB,且使得OM=ON,OA=OB;
2.連線AN與BM,他們相交於點P;
3.作射線OP。
則射線OP為角AOB的角平分線。
角平分線的定理:
角平分線的定理:
在角平分線上的點到這個角的兩邊的距離相等。
角平分線的逆定理:
在一個角的內部(包括頂點)且到角的兩邊距離相等的點,在這個角的平分線上。
畫平分線的注意事項:
注意兩個角要相等。
