內角平分線定理

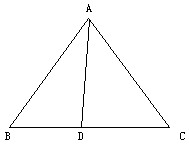
角平分線的性質定理．其內容是 三角形內角平分段性質定理 ∵AD平分∠BAC，∠BAD=∠DAC，

內角平分線定理圖

內角平分線定理　
角平分線的性質定理．其內容是
性質1 在角平分線上的點到這個角的兩邊的距離相等．
性質2 到一個角的兩邊的距離相等的點，在這個角的平分線上．
綜合定理1，2可得如下結論：
角的平分線是到角的兩邊距離相等的所有點的集合．
三角形內角平分段性質定理 三角形內角平分線分對邊所成的兩條線段，和兩條鄰邊成比例．
即
在三角形ABC中，當AD是頂角A的角平分線交底邊於D時，BD:DC=AB:AC.
證明：如圖，過點C作CE∥AD交BA的延長線於E，則DB/DC=AB/ae。
∵CE∥AD，
∴∠DAC=∠ACE，∠BAD=∠AEC。
∵AD平分∠BAC，∠BAD=∠DAC，
∴∠ACE=∠AEC，AE=AC。
∴DB/DC=AB/AE=AB/AC。