萊布尼茨三角形

1676年11月，他得出了公式 1673年左右，他獨立地得到了sin 這一年，萊布尼茨發表了他的第一篇數學論文《

簡述

微積分 1666年，萊布尼茨寫成“論組合術”(De ArtCombinatoria)一文，討論了平方數序列
0，1，4，9 16，…
的性質，例如它的第一階差為
1，3，5，7，…，
第二階差則恆等於
2，2，2，…
等．他注意到，自然數列的第二階差消失，平方序列的第三階差消失，等等．同時他還發現，如果原來的序列是從0開始的，那么第一階差之和就是序列的最後一項，如在平方序列中，前5項的第一階差之和為 1+3+5 +7=16，即序列的第5項．他用X表示序列中項的次序，用Y表示這一項的值．這些討論為他後來創立微積分奠定了初步思想，可以看作是他微積分思想的萌芽．“論組合術”是他的第一篇數學論文，使他躋身於組合數學研究者之列．

激發興趣

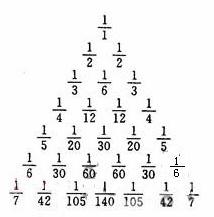
1672年，惠更斯給萊布尼茨出了一道他自己正同別人競賽的題目：求三角級數(1，3，6，10，…)倒數的級數之和
萊布尼茨圓滿地解決了這一問題，他是這樣計算的：
初次成功激發了他進一步深入鑽研數學的興趣．通過惠更斯，他了解到B．卡瓦列里(Cavalieri)、I．巴羅(Barrow)、B．帕斯卡(Pascal)、J．沃利斯(Wallis)的工作．於是，他開始研究求曲線的切線以及求平面曲線所圍圖形的面積、立體圖形體積等問題．1674年，他學習R．笛卡兒(Descartes)幾何學，同時對代數性發生了興趣．這一時期，他檢索了已有的數學文獻．
對於當時數學界密切關注的切線問題和求積問題，萊布尼茨在前人的基礎上提出了一個普遍方法．這個方法的核心是特徵三角形(characteristic triangle)．在帕斯卡、巴羅等人討論過的特徵三角形的基礎上，他建立了由dx，dy和PQ(弦)組成的特徵三角形．其中dx，dy的意義是這樣的：在他1666年“論組合術”中所考慮的序列中，用dx表示相鄰的序數之差，dy表示兩個相鄰項值之差，然後在數列項的順序中插入若干dx，dy，於是過渡到了任意函式的dx，dy．特徵三角形的兩條邊就是任意函式的dx，dy；而PQ 則是“P和 Q之間的曲線，而且是T點的切線的一部分”．如圖1，T是曲線y=f(x)上的一點，dx，dy分別是橫坐標、縱坐標的差值．

初步思想

利用這個特徵三角形，他很快就意識到兩個問題：
(1)曲線的切線依賴於縱坐標的差值與橫坐標的差值(當這些差值變成無窮小時)之比．通過考慮圖1中△pqr和△STU，發現△PQR∽△STU，從而有dy/dx=Tu/Su．也就是說，曲線y上過T點的切線的斜率是dy/dx．
(2)求積(面積)依賴於橫坐標的無限小區間的縱坐標之和或無限窄矩形之和．
有了這些思想，他很快就推導出了一大批新結論．用他自己的話說就是，從特徵三角形出發，“毫不費力，我確立了無數的定理”
根據萊布尼茨留下的遺稿可以判定，他是在1673年建立起特徵三角形思想的．他將特徵三角形的斜邊PQ用“dS”表示，這樣特徵三角形又稱為微分三角形(differential triangle)其中 ds2=dx2+dy2．
利用特徵三角形，萊布尼茨早在1673年就通過積分變換，得到了平面曲線的面積公式
這一公式是從幾何圖形中推導出來的，經常被他用來求面積．
1673—1674年，他給出了求一條曲線y=y(x)繞x軸鏇轉一周所形成的鏇轉體的表面積A的公式
同時，他還給出了曲線長度公式
在求面積問題方面，萊布尼茨深受卡瓦列里“線由無窮多個點構成，面由無窮多條線構成”思想的影響，認為曲線下的面積是無窮多的小矩形之和．1675年10月29日，他用“∫”代替了以前的和符號“OMN”(“∫”是Sum 和)的第一個字母“s”的拉長)，用∫ydx表示面積，在這份手稿中，他還從求積出發，得到了分部積分公式

得出公式

1676年11月，他得出了公式
其中n是整數或分數(n≠-1)．
萊布尼茨的積分方面的工作是與微分方面的工作交叉進行的．
由於研究巴羅的著作，以及引入特徵三角形，萊布尼茨越來越強烈地意識到，微分(主要是導數、求切線)與積分(求和)必定是相反的過程．在1675年10月29日的手稿中，他就注意到，面積被微分時必定給出長度，因此他開始探討“∫”的運算(積分)和“d”的運算(微分)之間的關係，認識到要從y回到dy，必須做出y的微差或者取y的微分．經過這種不充分的討論，他斷定一個事實：作為求和的過程的積分是微分的逆．這樣，萊布尼茨就第一次表達出了求和(積分)與微分之間的關係．
萊布尼茨於1675—1676年給出了微積分基本定理(後來又稱為牛頓-萊布尼茨公式)
(A為曲線f下的圖形的面積．)
於1693年給出了這個定理的證明．以前，微分和積分作為兩種數學運算、兩類數學問題，是分別地加以研究的．卡瓦列里、巴羅、沃利斯等許多人得到了一系列求面積(積分)、求切線斜率(導數)的重要結果，但這些結果是孤立、不連貫的．雖然他們已開始考慮微分和積分之間的關係，然而只有萊布尼茨和牛頓(各自獨立地)將微分和積分真正溝通起來，明確地找到了兩者的內在的直接聯繫：微分和積分是互逆的兩種運算．而這正是建立微積分學的關鍵所在．只有確立了這一基本關係，才能在此基礎上構建系統的微積分學．並從對各種函式的微分和求積公式中，總結出共同的算法程式，使微積分方法普遍化，發展成用符號表示的微積分運算法則．

發表論文

萊布尼茨於1684年10月發表在《教師學報》(Acta erudito-rum)上的論文，題目是“一種求極大值與極小值和求切線的新方法，它也適用於無理量，以及這種新方法的奇妙類型的計算”(Nova Methodus pro Maximis et Minimis，itemque tangentibus，quae necfractas，necirrationales quantitates moratur，et singularepro illis Calculi genus)，在數學史上被公認為是最早發表的微積分文獻．

函式微分

早在1677年7月11日前後及11月左右，萊布尼茨明確定義了dy為函式微分，給出了dy的演算規則：
“如果a是給定的常數，則da=0，dax=adx；
加法和減法 v=z—y+w+x，dv=dz-dy+dw+dx；
乘法 y=vx，dy=vdx+xdv
在1676—1677年的手稿中，他利用特徵三角形分析了曲線切線的變化情況：對於曲線v=v(x)，當dv與dx之比為無窮大時，切線垂直於坐標軸(x軸)．當dv與dx之比等於0時，切線平行於x軸，當dv=dx≠0時，則切線與坐標軸成45°角，他指出，對於曲線v，當dv=0時，“在這個位置的v，明顯地就是極大值(或極小值)”，他詳細討論了當dv<0，而變成dv=0後又dv<0時取極大值，反之則取極小值的情形．他還給出了拐點——曲線的凹凸情況發生變法的條件是d2v=0．
以後，萊布尼茨具體求出了各種各樣複雜函式的微商(導數)．1686年，給出了對數函式，指數函式的微商．1695年求出了y=xx的微商dy=xx(1+lnx)，等等．

萊布尼茨法則

他引入了n階微分的符號dn，並且給出了高階微分的“萊布尼茨法則”：
其中
n！=1×2×3×…×(n-1)×n．
萊布尼茨在積分方面的成就，後來比較集中地寫在1686年5月發表在《教師學報》上的一篇論文中，題為“潛在的幾何與不可分量和無限的分析”(De Geometria recondita et Analysi Indivisi-bilium atque Infinitorum)．
品中出現了積分符號．同年，他引入了空間曲線的“密切”(osculating)這一術語，並給出了曲率ρ公式：
其中R為曲率半徑．
1692年和1694年，他給出了求一族曲線 f(x，y，α)=0(α為曲線族參數)包絡的普遍方法：在
中消去α．實際上，用微積分方法研究幾何在微積分奠基者(牛頓、萊布尼茨等)那裡已經開始了．切線、包絡等幾何問題在萊布尼茨手中是與微積分連在一起的．

無窮級數

在微積分的早期研究中，有些函式如指數函式等超越函式的處理相當困難，然而人們發現，若用它們的級數來處理，則非常有成效．因此，無窮級數從一開始就是萊布尼茨、牛頓等人微積分工作的一個重要部分．有時使用無窮級數是為了計算一些特殊的量，如萊布尼茨曾用無窮級數表達式計算π(圓周率)．
在求面積的過程中，通過無窮級數表示圓在第一象限的面積，他得到了π的一個十分漂亮的表達式
1673年左右，他獨立地得到了sinx，cosx和arctgx等函式的無窮級數展開式．還得到了圓面積和雙曲線面積的具體展開式，並且將這些展開式與反正切、餘割、正弦函式、自然對數函式、指數函式聯繫起來了．他經常利用級數展開式研究超越函式．有時還將多項式定理用於分式函式或超越函式的展開式．
無窮級數展開式，得到了如下的式子：
誤的．直到1734—1735年，L．歐拉(Euler)才得到
在1713年10月25日寫給約翰?伯努利(John Bernoulli)的信中，萊布
“萊布尼茨判別法”，但他當時的證明卻錯了．在考慮級數 還相當混亂．
微分方程 微分方程在微積分創立之初就為人們所關注．1693年，萊布尼茨稱微分方程為特徵三角形的邊(dx，dy)的函式．在微分方程方面，他進行了一系列工作．其中有些工作是十分獨特的．
1691年，他提出了常微分方程的分離變數法，解決了形如
型方程的求解問題．方法是，先寫成
然後兩邊積分．
這一年，他還提出了求解一次齊次方
的方法：
因此經過這種變換，原來的一次齊次方程就變成了
1694年，他證明了把一階線性常微分方程y′+P(x)y=Q(x)化成積分方程的正確方法，他的方法使用了因變數替換．同時，他還給出了(y′)2+p(x)y′+q(x)=0的解法．1694年，他和約翰?伯努利引進了找等交曲線或曲線族的問題，並求出了一些特殊問題的解．
1696年，他證明了，利用變數替換z=y1-n，可以將伯努利方程
變換x=P11u+P12v，y=P21u+P22v可以將微分方程
a00+a10x+(a01+a11x)y′=0
進行簡化．
通過求解微分方程，萊布尼茨解決了許多具體問題．例如，1686年，他解決了這樣的問題：求一條曲線，使得一個擺沿著它作一次完全振動，都用相等的時間，而無論擺所經歷的弧長怎樣(即等時問題)．他指出，
證明，並認識到了圓函式、三角函式的超越性，弄清了許多超越函式的基本性質．此外，他還考慮過機率方程．這一時期，他還求出了十分重要的曳物線方程：
1691年，他給出了自達?芬奇(L．Da Vinci)時代就考慮過的懸鏈線(catenary，這個名稱是萊布尼茨給出的)方程為
1696年，約翰?伯努利提出了著名的最速降線問題：
求從一給定點到不是在它垂直下方的另一點的一條曲線，使得一質點沿這條曲線從給定點P1下滑所用的時間最短；其中摩擦和空氣阻力都忽略．
這是約翰?伯努利向全歐洲數學家發出的挑戰．1697年，萊布尼茨和I．牛頓(Newton)、G．F．A．洛比達(L’Hospital)、約翰?伯努利分別解決了最速降線問題，指出這是由方程
表示的上凹的鏇輪線，並由此開始了變分法的研究．
數學符號、代數 萊布尼茨在微積分方面的貢獻突出地表現在他發明了一套適用的符號系統．1675年引入dx表示x的微分，“∫”表示積分，ddv，dddy表示二階、三階微分．1695年左右用dmn表示m階微分．他比別人更早更明確地認識到，好的符號能大大節省思維勞動，運用符號的技巧是數學成功的關鍵之一．他自覺地和格外慎重地引入每一個數學符號，常常對各種符號進行長期的比較研究，然後再選擇他認為最好的、富有啟示性的符號．他創設的符號還有
此外還有對數符號、函式符號、行列式符號等等．很多符號的普遍使用與他的提倡和影響密切相關．他還引入了“函式”(function)、“常量”(constant quantity)、變數”(variate)、“參變數”(para-meter)等術語．
在代數學方面，萊布尼茨不僅強調引入符號的重要性，而且還討論了負數、複數的性質，認為複數的出現是無害的，斷言複數的對數是不存在的，為此曾在當時的數學界掀起了一場關於負數、虛數的對數之爭論．在研究複數時，他還得出過這樣的結論：共軛複數的和是實數
用一般的複數表示．他把虛數看作是存在(being)與非存在(not-being)的中介．
在1678年以前，萊布尼茨就開始了對線性方程組、行列式的研究，對消元法從理論上進行了探討．在1693年4月28日致洛比達的信中他提出了行列式概念：“我引進方程：
此處，在兩個數碼中，前者表示此數所屬的方程式，後者代表此數所屬的字母(未知數)．”這樣，他創設了採用兩個數碼的係數記號，相當於現在的aik，為矩陣和行列式一般理論的發展提供了方便的工具．

萊布尼茨其人

生平事跡

公元1646年7月1日，戈特弗里德·威廉·凡·萊布尼茨出生於德國東部萊比錫的一個書香之家，父親弗里德希·萊布尼茨是萊比錫大學的道德哲學教授，母親凱薩琳娜·施馬克出身於教授家庭，虔信路德新教。　萊布尼茨的父母親自做孩子的啟蒙教師，耳濡目染使萊布尼茨從小就十分好學，並有很高的天賦，幼年時就對詩歌和歷史有著濃厚的興趣。不幸的是，父親在他6歲時去世，卻給他留下了豐富藏書。　萊布尼茨的父親在他年僅六歲時便去世了，給他留下了比金錢更寶貴的豐富的藏書，知書達理的母親擔負起了兒子的幼年教育。萊布尼茨因此得以廣泛接觸古希臘羅馬文化，閱讀了許多著名學者的著作，由此而獲得了堅實的文化功底和明確的學術目標。　8歲時，萊布尼茨進入尼古拉學校，學習拉丁文、希臘文、修辭學、算術、邏輯、音樂以及《聖經》、路德教義等。　1661年，15歲的萊布尼茨進入萊比錫大學學習法律，一進校便跟上了大學二年級標準的人文學科的課程，他還抓緊時間學習哲學和科學。1663年5月，他以《論個體原則方面的形上學爭論》一文獲學士學位。這期間萊布尼茨還廣泛閱讀了培根、克卜勒、伽利略等人的著作，並對他們的著述進行深入的思考和評價。在聽了教授講授的歐幾里得的《幾何原本》的課程後，萊布尼茨對數學產生了濃厚的興趣。　1664年1月，萊布尼茨完成了論文《論法學之艱難》，獲哲學碩士學位。是年2月12日，他母親不幸去世。18歲的萊布尼茨從此隻身一人生活，他—生在思想、性格等方面受母親影響頗深。　1665年，萊布尼茨向萊比錫大學提交了博士論文《論身份》，1666年，審查委員會以他太年輕(年僅20歲)而拒絕授予他法學博士學位，黑格爾認為，這可能是由於萊布尼茨哲學見解太多，審查論文的教授們看到他大力研究哲學，心裡很不樂意。他對此很氣憤，於是毅然離開萊比錫，前往紐倫堡附近的阿爾特多夫大學，並立即向學校提交了早已準備好的那篇博士論文，1667年2月，阿爾特多夫大學授予他法學博士學位，還聘請他為法學教授。　這一年，萊布尼茨發表了他的第一篇數學論文《論組合的藝術》。這是一篇關於數理邏輯的文章，其基本思想是想把理論的真理性論證歸結於一種計算的結果。這篇論文雖不夠成熟，但卻閃耀著創新的智慧和數學的才華，後來的一系列工作使他成為數理邏輯的創始人。　1666年，萊布尼茨獲得法學博士學位後，在紐倫堡加入了一個鍊金術士團體，1667年，通過該團體結識了政界人物博因堡男爵約翰·克里斯蒂文，並經男爵推薦給選帝侯邁因茨，從此萊布尼茨登上了政治舞台，便投身外交界，在美因茨大主教舍恩博恩的手下工作。　167l～1672年冬季，他受邁因茨選帝侯之託，著手準備制止法國進攻德國的計畫。1672年，萊布尼茨作為一名外交官出使巴黎，試圖遊說法國國王路易十四放棄進攻，卻始終未能與法王見上一面，更談不上完成選帝侯交給他的任務了。這次外交活動以失敗而告終，然而在這期間，他深受惠更斯的啟發，決心鑽研高等數學，並研究了笛卡兒、費爾馬、帕斯卡等人的著作，開始創造性的工作。　1673年1月，為了促使英國與荷蘭之間的和解，他前往倫敦進行斡鏇未果。他卻趁這個機會與英國學術界知名學者建立了聯繫。他見到了與之通信達三年的英國皇家學會秘書、數學家奧登伯以及物理學家胡克、化學家波義耳等人。1673年3月萊布尼茨回到巴黎，4月即被推薦為英國皇家學會會員。這一時期，他的興趣越來越明顯地表現在數學和自然科學方面。　1672年10月，邁因茨選帝侯去世，萊布尼茨失去了職位和薪金，而僅是一位家庭教師了。當時，他曾多方謀求外交官的正式職位，或者希望在法國科學院謀一職位，都沒有成功。無奈，只好接受漢諾瓦公爵約翰·弗里德里希的邀請，前往漢諾瓦。　1676年10月4日，萊布尼茨離開巴黎，他先在倫敦作了短暫停留。繼而前往荷蘭，見到了使用顯微鏡第一次觀察了細菌、原生動物和精子的生物學家列文虎克，這些對萊布尼茨以後的哲學思想產生了影響。在海牙，他見到了斯賓諾莎。1677年1月，萊布尼茨抵達漢諾瓦，擔任布倫茲維克公爵府法律顧問兼圖書館館長和布倫茲維克家族史官，並負責國際通信和充當技術顧問。漢諾瓦成了他的永久居住地。　在繁忙的公務之餘，萊布尼茨廣泛地研究哲學和各種科學、技術問題，從事多方面的學術文化和社會政治活動。不久，他就成了宮廷議員，在社會上開始聲名顯赫，生活也由此而富裕。1682年，萊布尼茨與門克創辦了近代科學史上卓有影響的拉丁文科學雜誌《學術紀事》(又稱《教師學報》)，他的數學、哲學文章大都刊登在該雜誌上；這時，他的哲學思想也逐漸走向成熟。　1679年12月，布倫茲維克公爵約翰·弗里德里卻突然去世，其弟奧古斯特繼任爵位，萊布尼茨仍保留原職。新公爵夫人蘇菲是他的哲學學說的崇拜者，“世界上沒有兩片完全相同的樹葉”這一句名言，就出自他與蘇菲的談話。　奧古斯特為了實現他在整個德國出人頭地的野心，建議萊布尼茨廣泛地進行歷史研究與調查，寫一部有關他們家庭近代歷史的著作。1686年他開始了這項工作。在研究了當地有價值的檔案材料後，他請求在歐洲作一次廣泛的遊歷。　1687年11月，萊布尼茨離開漢諾瓦，於1688年初夏5月抵達維也納。他除了查找檔案外，大量時間用於結識學者和各界名流。在維也納，他拜見了奧地利皇帝利奧波德一世，為皇帝構畫出一系列經濟、科學規劃，給皇帝留下了深刻印象。他試圖在奧地利宮庭中謀一職位，但直到1713年才得到肯定答覆，而他請求古奧地利建立一個“世界圖書館”的計畫則始終未能實現。隨後，他前往威尼斯，然後抵達羅馬。在羅馬，他被選為羅馬科學與數學科學院院士。1690年，萊布尼茨回到了漢諾瓦。由於撰寫布倫茲維克家族歷史的功績，他獲得了樞密顧問官職務。　在1700年世紀轉變時期，萊布尼茨熱心地從事於科學院的籌劃、建設事務。他覺得學者們各自獨立地從事研究既浪費了時間又收效不大，因此竭力提倡集中人才研究學術、文化和工程技術，從而更好地安排社會生產，指導國家建設。　從1695年起，萊布尼茨就一直為在柏林建立科學院四處奔波，到處遊說。1698年，他為此親自前往柏林。1700年，當他第二次訪問柏林時，終於得到了弗里德里希一世，特別是其妻子(漢諾瓦奧古斯特公爵之女)的贊助，建立了柏林科學院，他出任首任院長。1700年2月，他還被選為法國科學院院士。至此，當時全世界的四大科學院：英國皇家學會、法國科學院、羅馬科學與數學科學院、柏林科學院都以萊布尼次作為核心成員。　1713年初，維也納皇帝授予萊布尼茨帝國顧問的職位，邀請他指導建立科學院。俄國的彼得大帝也在17ll～1716年去歐洲旅行訪問時，幾次聽取了萊布尼茨的建議。萊布尼茨試圖使這位雄才大略的皇帝相信，在彼得堡建立一個科學院是很有價值的。彼得大帝對此很感興趣，1712年他給了萊布尼茨一個有薪水的數學、科學宮廷顧問的職務。1712年左右，他同時被維出納、布倫茲維克、柏林、彼得堡等王室所雇用。這一時期他一有機會就積極地鼓吹他編寫百科全書，建立科學院以及利用技術改造社會的計畫。在他去世以後，維也納科學院、彼得堡科學院先後都建立起來了。據傳，他還曾經通過傳教士，建議中國清朝的康熙皇帝在北京建立科學院。　就在萊布尼茨倍受各個宮廷青睞之時，他卻已開始走向悲慘的晚年了。公元1716年11月14日，由於膽結石引起的腹絞痛臥床一周后，萊布尼茨孤寂地離開了人世，終年70歲。　萊布尼茨一生沒有結婚，沒有在大學當教授。他平時從不進教堂，因此他有一個綽號 Lovenix，即什麼也不信的人。他去世時教士以此為藉口，不予理睬，曾雇用過他的宮廷也不過問，無人前來弔唁。彌留之際，陪伴他的只有他所信任的大夫和他的秘書艾克哈特。艾克哈特發出訃告後，法國科學院秘書封登納爾在科學院例會時向萊布尼茨這位外國會員致了悼詞。1793年，漢諾瓦人為他建立了紀念碑；1883年，在萊比錫的一座教堂附近豎起了他的一座立式雕像；1983年，漢諾瓦市政府照原樣重修了被毀於第二次世界大戰中的“萊布尼茨故居”，供人們瞻仰。

個人成就

始創微積分　17世紀下半葉，歐洲科學技術迅猛發展，由於生產力的提高和社會各方面的迫切需要，經各國科學家的努力與歷史的積累，建立在函式與極限概念基礎上的微積分理論應運而生了。　微積分思想，最早可以追溯到希臘由阿基米德等人提出的計算面積和體積的方法。1665年牛頓創始了微積分，萊布尼茨在1673—1676年間也發表了微積分思想的論著。　以前，微分和積分作為兩種數學運算、兩類數學問題，是分別的加以研究的。卡瓦列里、巴羅、沃利斯等人得到了一系列求面積(積分)、求切線斜率(導數)的重要結果，但這些結果都是孤立的，不連貫的。　只有萊布尼茨和牛頓將積分和微分真正溝通起來，明確地找到了兩者內在的直接聯繫：微分和積分是互逆的兩種運算。而這是微積分建立的關鍵所在。只有確立了這一基本關係，才能在此基礎上構建系統的微積分學。並從對各種函式的微分和求積公式中，總結出共同的算法程式，使微積分方法普遍化，發展成用符號表示的微積分運算法則。因此，微積分“是牛頓和萊布尼茨大體上完成的，但不是由他們發明的”。　然而關於微積分創立的優先權，在數學史上曾掀起了一場激烈的爭論。實際上，牛頓在微積分方面的研究雖早於萊布尼茨，但萊布尼茨成果的發表則早於牛頓。　萊布尼茨1684年10月在《教師學報》上發表的論文《一種求極大極小的奇妙類型的計算》，是最早的微積分文獻。這篇僅有六頁的論文，內容並不豐富，說理也頗含糊，但卻有著劃時代的意義。　牛頓在三年後，即1687年出版的《自然哲學的數學原理》的第一版和第二版也寫道：“十年前在我和最傑出的幾何學家萊布尼茨的通信中，我表明我已經知道確定極大值和極小值的方法、作切線的方法以及類似的方法，但我在交換的信件中隱瞞了這方法，……這位最卓越的科學家在回信中寫道，他也發現了一種同樣的方法。他並訴述了他的方法，它與我的方法幾乎沒有什麼不同，除了他的措詞和符號而外”（但在第三版及以後再版時，這段話被刪掉了）。　因此，後來人們公認牛頓和萊布尼茨是各自獨立地創建微積分的。