簡介
 旋輪線
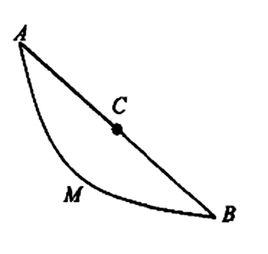
旋輪線在一個斜面上,擺兩條軌道,一條是直線,一條是曲線,起點高度以及終點高度都相同。兩個質量、大小一樣的小球同時從起點向下滑落,曲線的小球反而先到終點。這是由於曲線軌道上的小球先達到最高速度,所以先到達。然而,兩點之間的直線只有一條,曲線卻有無數條,那么,哪一條才是最快的呢?伽利略於1630年提出了這個問題,當時他認為這條線應該是一條圓弧,可是後來人們發現這個答案是錯誤的。1696年,瑞士數學家約翰·伯努利解決了這個問題,他還拿這個問題向其他數學家提出了公開挑戰。牛頓、萊布尼茲、洛比達以及雅克布·伯努利等解決了這個問題。這條最速降線就是一條擺線,也叫旋輪線(連線兩個點上凹的唯一一段旋輪線)。
旋輪線與1673年荷蘭科學家惠更斯討論的擺線相同。因為鐘錶擺錘作一次完全擺動所用的時間相等,所以擺線(旋輪線)又稱等時曲線。
看一個稍微有點振奮人心的東西,約翰·伯努利對最速降線問題的非常精妙的解答:
如果使分成的層數n無限地增加,即每層的厚度無限地變薄,則質點的運動便趨於空間A、B兩點間質點運動的真實情況,此時折線也就無限增多,其形狀就趨近我們所要求的曲線——最速降線.而折線的每一段趨向於曲線的切線,因而得出最速降線的一個重要性質:任意一點上切線和鉛垂線所成的角度的正弦與該點落下的高度的平方根的比是常數.而具有這種性質的曲線就是擺線.所謂擺線,它是一個圓沿著一條直線滾動正(無滑動)時,圓周上任意一點的軌跡。
因此,最速降線就是擺線,只不過在最速降線問題中,這條擺線是上、下顛倒過來的罷了.
證明
列出表達式
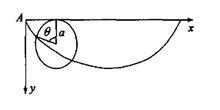
設 O, A是高度
不同,且不在同一鉛垂線上的兩定點, y
如果不計摩擦和空氣阻力,一質點 m
在重力作用下從 O點沿一曲線降落至 。 A( p, q) A點,問曲線呈何種形狀時,質點降 y
落的時間最短。
圖 7-1 設曲線為 y = y( x) ,坐標如圖 7-1,質點由 O點開始運動,它的速度 v與它的縱坐標有關係
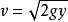 最速降線問題
最速降線問題式中, g是重力加速度。
在曲線上點 ( x, y) 處,質點的運動速度為
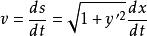 最速降線問題
最速降線問題式中, s表示曲線的弧長, t表示時間,於是
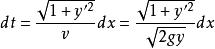 最速降線問題
最速降線問題由於點 O, A的橫坐標分別是 0, p,則質點 m從 O點運動到 A點所需時間為
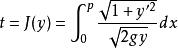 最速降線問題
最速降線問題(7.1.4)
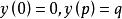 最速降線問題
最速降線問題這樣,質點由 O點運動到 A點所需時間 t是 y( x)的函式,最速降線問題就是滿足邊界條件的 所有連續函式 y( x)中,求出一個函式 y使泛函式(7.1.4)取最小值。
對泛函求極值的問題稱為變分問題,使泛函取極值的函式稱為變分問題的解,也稱為極值函式。
在微分學中,求函式 y = y( x) 的極值是求自變數 x的值,當 x取這些值時, y取極 大(小)值、取極值的必要條件是d y/d x= 0 。下面我們仿照函式微分的概念來定義泛函的變分概念,進而導出泛函極值存在的必要條件。設 y, y是集合 C的元素,稱δ y = y − y 為函式 y在 y0處的變分。
這裡的δ y是 x的函式,它與 ∆ y的區別在於:變分 δ y反映的是整個函式的改變,
而 ∆ y表示的是同一個函式 y( x)因 x的不同值而產生的差異。在本書,我們總是假定 y( x)和 F( x, y, y′) 都是充分光滑的,且 y( x)在兩個端點處固定,即
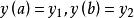 最速降線問題
最速降線問題(7.1.5)
式中, y, y是兩個常數。
考慮泛函
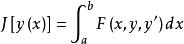 最速降線問題
最速降線問題(7.1.6)
當函式 y( x)有微小改變且變為 y( x) +δ y( x) 時,利用
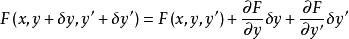 最速降線問題
最速降線問題上式可推出
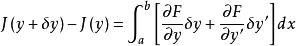 最速降線問題
最速降線問題上式稱為 J ( y)的變分,記為δ J ( y),即
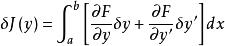 最速降線問題
最速降線問題(7.1.7)
下面我們證明,泛函 J ( y)取極值的必要條件是
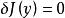 最速降線問題
最速降線問題(7.1.8)
或者
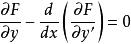 最速降線問題
最速降線問題(7.1.9)
設 y = y( x) 使泛函 J ( y)取極值,取函式 y( x)變分的特殊形式為
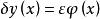 最速降線問題
最速降線問題式中, ε是任意小的實數;ϕ( x)是充分光滑的任意函式,並且滿足條件
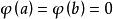 最速降線問題
最速降線問題這樣,函式
y( x) +εϕ( x) 滿足邊界條件式(7.1.5)。因此,泛函 J[ y( x) +εϕ( x)]
當 ε= 0時取最小值 J[ y( x)] ,從而有
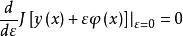 最速降線問題
最速降線問題由於
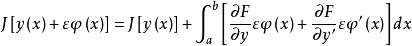 最速降線問題
最速降線問題則有
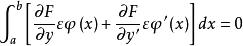 最速降線問題
最速降線問題(7.1.10)
則有
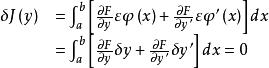 最速降線問題
最速降線問題套用分部積分,我們作進一步的分析,有
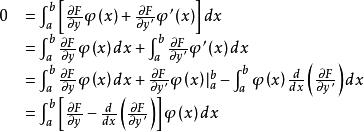 最速降線問題
最速降線問題由ϕ( x)的任意性,可得
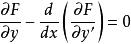 最速降線問題
最速降線問題(7.1.11)
式(7.1.11)稱為歐拉-拉格朗日方程,簡記為 E-L方程,
必要條件
y = y( x) 使泛函式(7.1.6)取極小值,則 y = y( x) 一定使歐拉-拉格朗日方程式(7.1.11)滿足邊界條件式(7.1.5)的解。
我們把滿足 E-L方程邊值問題的解稱為駐留函式,對應的積分曲線稱為駐留曲線。嚴格地講,E-L方程邊值問題的解滿足變分問題的必要條件,因此它是否是極值函式,還需作進一步的判別。在實際問題中,極值的存在性通常給出問題時已經肯定了,這樣,當一個實際現象已知其有唯一的極值存在,而這時也只得到一個駐留函式,則可以判定這個駐留函式就是極值函式。
最終解答
解
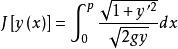 最速降線問題
最速降線問題且y(0)=0,y(p)=q
這樣
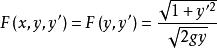 最速降線問題
最速降線問題(7.1.12)
其E-L方程為
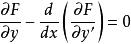 最速降線問題
最速降線問題由於
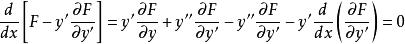 最速降線問題
最速降線問題所以有
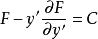 最速降線問題
最速降線問題(7.1.13)
將(7.1.12)代入式(7.1.13)
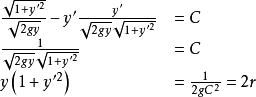 最速降線問題
最速降線問題(7.1.14)
引入變數代換x=x(θ),並設y'=cot(θ/2)
則由式(7.1.14)可得
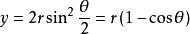 最速降線問題
最速降線問題上式對θ求導,得
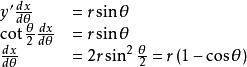 最速降線問題
最速降線問題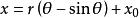 最速降線問題
最速降線問題所以
根據曲線過原點(0,0)及(p,q)可求出x0=0及r,這樣,所求曲線為
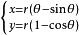 最速降線問題
最速降線問題