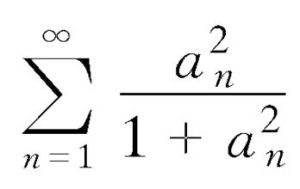級數
定義
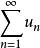 絕對收斂
絕對收斂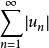 絕對收斂
絕對收斂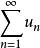 絕對收斂
絕對收斂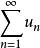 絕對收斂
絕對收斂如果級數 各項的絕對值所構成的級數 收斂,則稱級數 絕對收斂,級數 稱為絕對收斂級數。
定理
定理1:絕對收斂級數一定收斂。
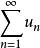 絕對收斂
絕對收斂定理2:設級數 絕對收斂,且其和等於S,則任意重排後所得的級數也絕對收斂,且有相同的和數。
注意:由條件收斂級數重排後所得的新級數,即使收斂,也不一定收斂於原來的和數。而且,條件收斂級數適當排列後,可得到發散級數,或收斂於事先任意指定的數。
定理3:若級數:
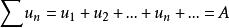 絕對收斂
絕對收斂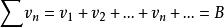 絕對收斂
絕對收斂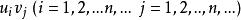 絕對收斂
絕對收斂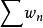 絕對收斂
絕對收斂都絕對收斂,則對所有乘積 按任意排列所得的級數 也絕對收斂,且其和等於AB。
判別方法
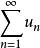 絕對收斂
絕對收斂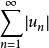 絕對收斂
絕對收斂由定義可知,要知道 是否絕對收斂,只需要看 是否收斂。下面將介紹5種判別級數是否收斂的方法。
(1)【阿貝爾判別法】
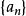 絕對收斂
絕對收斂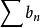 絕對收斂
絕對收斂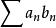 絕對收斂
絕對收斂若 為單調有界數列,且級數 收斂,則級數 收斂。
(2)【狄利克雷判別法】
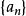 絕對收斂
絕對收斂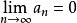 絕對收斂
絕對收斂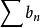 絕對收斂
絕對收斂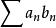 絕對收斂
絕對收斂若數列 單調遞減,且 ,又級數 的部分和數列有界,則級數 收斂。
(3)【比式判別法】
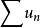 絕對收斂
絕對收斂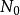 絕對收斂
絕對收斂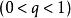 絕對收斂
絕對收斂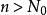 絕對收斂
絕對收斂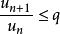 絕對收斂
絕對收斂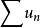 絕對收斂
絕對收斂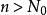 絕對收斂
絕對收斂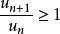 絕對收斂
絕對收斂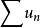 絕對收斂
絕對收斂設 為正項級數,且存在某正整數 及常數q 。若對一切 ,不等式 成立,則級數 收斂;若對一切 ,不等式 成立,則級數 發散。
【推論】
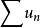 絕對收斂
絕對收斂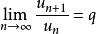 絕對收斂
絕對收斂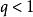 絕對收斂
絕對收斂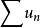 絕對收斂
絕對收斂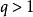 絕對收斂
絕對收斂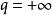 絕對收斂
絕對收斂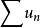 絕對收斂
絕對收斂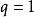 絕對收斂
絕對收斂設 為正項級數,且 ,則若 時,級數 收斂;若 或 時,級數 發散;若 ,則無法判斷。
(4)【根式判別法】
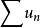 絕對收斂
絕對收斂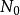 絕對收斂
絕對收斂 絕對收斂
絕對收斂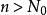 絕對收斂
絕對收斂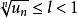 絕對收斂
絕對收斂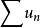 絕對收斂
絕對收斂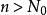 絕對收斂
絕對收斂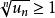 絕對收斂
絕對收斂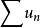 絕對收斂
絕對收斂設 為正項級數,且存在某正整數 及正常數 。若對一切 ,不等式 成立,則級數 收斂;若對一切 ,不等式 成立,則級數 發散。
【推論】
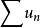 絕對收斂
絕對收斂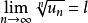 絕對收斂
絕對收斂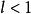 絕對收斂
絕對收斂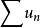 絕對收斂
絕對收斂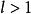 絕對收斂
絕對收斂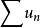 絕對收斂
絕對收斂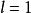 絕對收斂
絕對收斂設 為正項級數,且 ,則若 時,級數 收斂;若 時,級數 發散;若 ,則無法判斷。
(5)【比較原則】
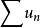 絕對收斂
絕對收斂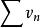 絕對收斂
絕對收斂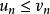 絕對收斂
絕對收斂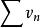 絕對收斂
絕對收斂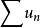 絕對收斂
絕對收斂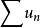 絕對收斂
絕對收斂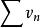 絕對收斂
絕對收斂設 和 是兩個正項級數,如果存在某個正數N,對一切n>N,都有: ,若級數 收斂,則,級數 也收斂;若級數 發散,則, 也發散。
無窮積分
定義
 絕對收斂
絕對收斂 絕對收斂
絕對收斂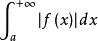 絕對收斂
絕對收斂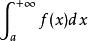 絕對收斂
絕對收斂1. 若函式 在任何有限區間 上可積,且無窮積分 收斂,則稱 絕對收斂。
 絕對收斂
絕對收斂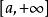 絕對收斂
絕對收斂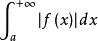 絕對收斂
絕對收斂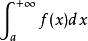 絕對收斂
絕對收斂2.函式在區間上連續,且無窮限積分收斂,則稱絕對收斂
定理
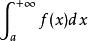 絕對收斂
絕對收斂 絕對收斂
絕對收斂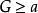 絕對收斂
絕對收斂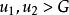 絕對收斂
絕對收斂1. 無窮積分 收斂的充要條件是:任給 ,存在 ,只要 ,便有:
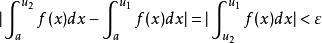 絕對收斂
絕對收斂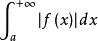 絕對收斂
絕對收斂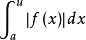 絕對收斂
絕對收斂2.收斂的充要條件是:存在上界
判定方法
(1)【比較判別法】
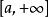 絕對收斂
絕對收斂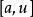 絕對收斂
絕對收斂設定義在上的兩個函式f 和 g 都在任意有限區間上可積,且滿足
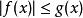 絕對收斂
絕對收斂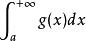 絕對收斂
絕對收斂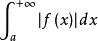 絕對收斂
絕對收斂則當收斂時,必定收斂。
(2)【狄利克雷判別法】
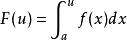 絕對收斂
絕對收斂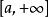 絕對收斂
絕對收斂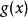 絕對收斂
絕對收斂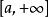 絕對收斂
絕對收斂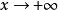 絕對收斂
絕對收斂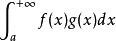 絕對收斂
絕對收斂若在上有界,在上當 時單調趨於0,則收斂。
(3)【阿貝爾判別法】
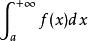 絕對收斂
絕對收斂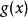 絕對收斂
絕對收斂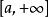 絕對收斂
絕對收斂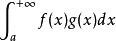 絕對收斂
絕對收斂若收斂,在上單調有界,則收斂。
無論無窮級數還是無窮積分,它們都是要么發散,要么條件收斂,要么絕對收斂,三者必居其一。