定義
針對數值級數
對於一個無條件收斂級數，把級數的各項相加的順序做任意的排列後所得到的各種級數仍收斂於同一極限。對數項級數而言，級數是無條件收斂的若且唯若級數是絕對收斂等價的。
在數項級數中，絕對收斂級數主要有兩個重要性質：
（1）級數的重排。若數項級數絕對收斂，其和等於S，則任意重排後所得到的級數也絕對收斂且有相同的和數。
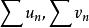無條件收斂級數（2）級數的乘積。若兩級數均為絕對收斂級數且分別收斂於A,B，則這兩個級數的乘積按正方形順序或按對角線順序排列所得的級數也是絕對收斂的，並且收斂於AB。
針對Banach空間內級數
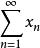無條件收斂級數
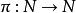無條件收斂級數
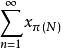無條件收斂級數 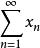無條件收斂級數是Banach空間內的級數，如果對每一個排列 ，級數 收斂，則稱 為無條件收斂的。
針對泛函級數
無條件收斂級數
無條件收斂級數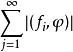
無條件收斂級數假如對任意基本函式，級數收斂，則稱泛函級數為無條件收斂的。
Hilbert空間內的無條件收斂
定理1
無條件收斂級數
無條件收斂級數設X為Banach空間， ，則級數 無條件收斂的充要條件是它的任一子級數收斂。
定理2
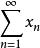無條件收斂級數
無條件收斂級數設Hilbert空間內的級數 是無條件收斂的，則 。
Lp空間內的無條件收斂
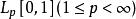無條件收斂級數 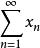無條件收斂級數
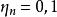無條件收斂級數
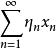無條件收斂級數設 空間內的級數 是無條件收斂，則對任何 ，級數 收斂。
引理
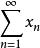無條件收斂級數
無條件收斂級數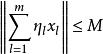
無條件收斂級數設 是Banach空間內的無條件收斂級數，則存在常數M>0，對一切的 有如下結論成立： 。
W.Orlicz定理
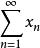無條件收斂級數
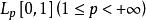無條件收斂級數如果級數 是 空間內的無條件收斂級數，則有：
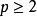無條件收斂級數
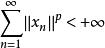無條件收斂級數（1）當時 ， ；
無條件收斂級數 無條件收斂級數（2）當時 ， 。
一致凸Banach空間內的無條件收斂
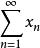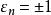無條件收斂級數
無條件收斂級數
無條件收斂級數設級數 是Banach空間內的無條件收斂級數，則對任何的 ，級數 是收斂的。
凸性模
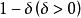無條件收斂級數
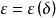無條件收斂級數
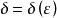無條件收斂級數在一致凸的Banach空間內，被單位球所截得的距球心距離是 平面直徑集合的上界記為 ，它的反函式 稱為空間的凸性模。
M.H.Kaneu定理
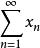無條件收斂級數 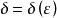無條件收斂級數
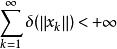無條件收斂級數如果級數 在一致凸Banach空間內是無條件收斂的，其凸性模 ，則有： 。
cotype p的Banach空間內的無條件收斂級數
cotype p的Banach空間內的無條件收斂級數的最新結果，包含了著名的W.orlicz的定理。
定理1
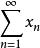無條件收斂級數
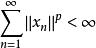無條件收斂級數設 是具有cotype p的Banach空間內的無條件收斂級數，則 。
定理2
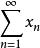無條件收斂級數
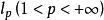無條件收斂級數設 是 空間內的無條件收斂級數，則有：
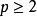無條件收斂級數 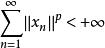無條件收斂級數（1）當時 ， ；
無條件收斂級數 無條件收斂級數（2）當時 ， 。
