定義
絕對收斂級數
絕對收斂級數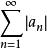 絕對收斂級數若任意數項級數的各項的絕對值組成的級數是收斂的，則稱級數是絕對收斂級數。
性質
1）絕對收斂的級數是收斂的，但是，收斂的級數不一定是絕對收斂的（非絕對收斂的收斂級數稱為條件收斂級數）；
絕對收斂級數2）若級數絕對收斂，則任意交換它的各項順序後所得的新級數也絕對收斂，且其和不變；
絕對收斂級數
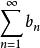絕對收斂級數
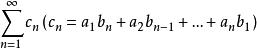絕對收斂級數3）若級數和都絕對收斂，其和分別為A與B，則級數也絕對收斂，其和等於AB。
判別法
1）比較判別法
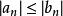絕對收斂級數
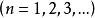絕對收斂級數設，
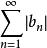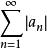絕對收斂級數 絕對收斂級數 絕對收斂級數①若級數收斂，則級數也收斂，即絕對收斂；
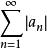絕對收斂級數 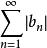絕對收斂級數 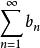絕對收斂級數②若級數發散，則級數也發散，即非絕對收斂。
2）比較判別法的極限形式
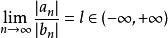絕對收斂級數設
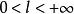絕對收斂級數 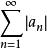絕對收斂級數 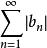絕對收斂級數①若，則級數與級數同時斂散；
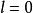絕對收斂級數 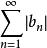絕對收斂級數 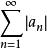絕對收斂級數②若，則級數收斂時，級數也收斂；
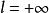絕對收斂級數 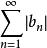絕對收斂級數 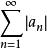絕對收斂級數③若，則當級數發散時，級數也發散。
3）比值判別法
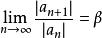絕對收斂級數設
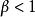絕對收斂級數 絕對收斂級數①當時，級數絕對收斂；
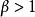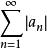絕對收斂級數 絕對收斂級數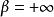 絕對收斂級數
絕對收斂級數 絕對收斂級數②當時，級數發散，級數也發散。特別地，當時，級數發散；
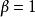絕對收斂級數③當時，比值判別法失效（即無法通過比值判別法判斷級數是否絕對收斂）。
4）Raabe判別法
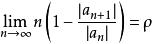絕對收斂級數設
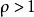絕對收斂級數 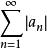絕對收斂級數①當時，級數收斂；
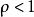絕對收斂級數 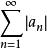絕對收斂級數②當時，級數發散。
