預備知識
數項級數的定義
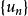 收斂級數
收斂級數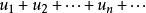 收斂級數
收斂級數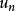 收斂級數
收斂級數給定一個數列 ,對它的各項依次用“+”號連線起來的表達式 “ ” 稱為數項級數,或稱為無窮級數,也可以簡稱為級數,其中 稱為數項級數的通項。
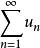 收斂級數
收斂級數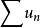 收斂級數
收斂級數上述數項級數常寫作: ,或者簡單記作 。
數項級數的前n項和
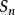 收斂級數
收斂級數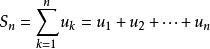 收斂級數
收斂級數數項級數的前 n 項和記作 ,且有 。
部分和數列
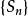 收斂級數
收斂級數 收斂級數
收斂級數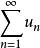 收斂級數
收斂級數稱數列 ,即數列 為數項級數 的部分和數列。
定義
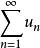 收斂級數
收斂級數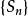 收斂級數
收斂級數 收斂級數
收斂級數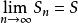 收斂級數
收斂級數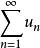 收斂級數
收斂級數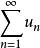 收斂級數
收斂級數 收斂級數
收斂級數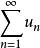 收斂級數
收斂級數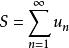 收斂級數
收斂級數若數項級數 的部分和數列 收斂於 (即 ),則稱數項級數 收斂,即 為收斂級數,且稱 為數項級數 的和,記作 。
收斂級數分條件收斂級數和絕對收斂級數兩大類,其性質與有限和(有限項相加)相比有本質的差別,例如交換律和結合律對它不一定成立,收斂級數概念是柯西於1821年引進的。
基本性質
性質1
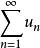 收斂級數
收斂級數 收斂級數
收斂級數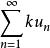 收斂級數
收斂級數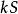 收斂級數
收斂級數設 k 為常數,如果級數 收斂於 ,則級數 也收斂,且收斂於 。
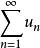 收斂級數
收斂級數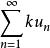 收斂級數
收斂級數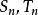 收斂級數
收斂級數證明:設級數 和 的部分和分別為 ,
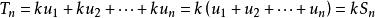 收斂級數
收斂級數則有 ,
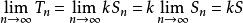 收斂級數
收斂級數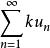 收斂級數
收斂級數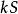 收斂級數
收斂級數於是 ,這就表明級數 也收斂,且收斂於 。
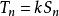 收斂級數
收斂級數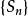 收斂級數
收斂級數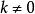 收斂級數
收斂級數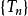 收斂級數
收斂級數註:由關係式 可知,如果數列 沒有極限且 ,那么 也沒有極限。由此我們得到結論:級數的每一項同乘一個不為零的常數後,它的收斂性不變。
性質2
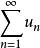 收斂級數
收斂級數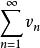 收斂級數
收斂級數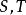 收斂級數
收斂級數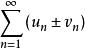 收斂級數
收斂級數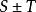 收斂級數
收斂級數如果級數 、 分別收斂於 ,則級數 也收斂,且收斂到 。
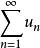 收斂級數
收斂級數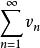 收斂級數
收斂級數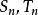 收斂級數
收斂級數證明:設級數 與 的部分和分別為 ,
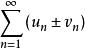 收斂級數
收斂級數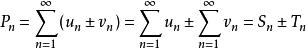 收斂級數
收斂級數則級數 的部分和為 ,
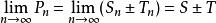 收斂級數
收斂級數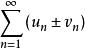 收斂級數
收斂級數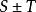 收斂級數
收斂級數於是 ,這就表明了級數 收斂,且收斂於 。
注意:性質2說明,兩個收斂級數逐項相加或逐項相減之後仍為收斂級數。
性質3
在級數中去掉、加上或改變有限項,不會改變級數的收斂性。
證明:我們只需證明“在級數的前面部分去掉、加上有限項,不會改變級數的收斂性”,因為其他情形(即在級數中去掉、加上或改變有限項的情形)都可以看成在級數的前面部分先去掉有限項,然後再加上有限項的結果。
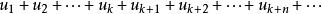 收斂級數
收斂級數以去掉k項為例,設級數為 ,
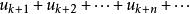 收斂級數
收斂級數去掉前 k 項,得到新的級數 ,
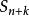 收斂級數
收斂級數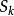 收斂級數
收斂級數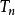 收斂級數
收斂級數記原級數前 k+n 項的和為 ,前 k 項和為 ,去掉前 k 項得到的新級數的前 n 項和為 ,
 收斂級數
收斂級數則有 。
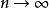 收斂級數
收斂級數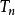 收斂級數
收斂級數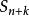 收斂級數
收斂級數易得當 時, 與 同時有極限,或者同時沒有極限,
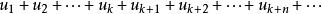 收斂級數
收斂級數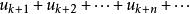 收斂級數
收斂級數即級數 與 同時收斂或同時發散。
類似的,可以證明在級數前面加上有限項,不會改變級數的收斂性。
性質4
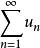 收斂級數
收斂級數若級數 收斂,則對此級數的項任意加括弧後所得的級數
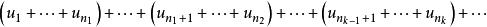 收斂級數
收斂級數仍然收斂,且其和不變。
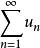 收斂級數
收斂級數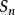 收斂級數
收斂級數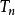 收斂級數
收斂級數證明:設級數 的前 n 項部分和 ,加括弧後所成的級數的前 k 項的和為 ,則有:
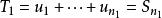 收斂級數
收斂級數,
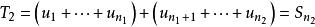 收斂級數
收斂級數,
...
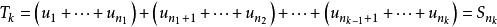 收斂級數
收斂級數,
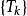 收斂級數
收斂級數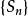 收斂級數
收斂級數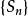 收斂級數
收斂級數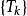 收斂級數
收斂級數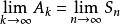 收斂級數
收斂級數可見,數列是數列的一個子數列。由數列的收斂性以及收斂子列與其子列的關係可知:數列必定收斂,且有。這說明了加括弧後所成的級數收斂,且其和不變。
注意:如果加括弧後所成的級數發散,則原級數也發散。
性質5
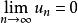 收斂級數
收斂級數如果級數收斂,則必有。
級數收斂性
等比級數(幾何級數)
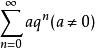 收斂級數
收斂級數等比級數 :
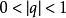 收斂級數
收斂級數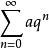 收斂級數
收斂級數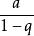 收斂級數
收斂級數(1)當 時,收斂,且收斂於;
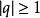 收斂級數
收斂級數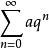 收斂級數
收斂級數(2)當時,發散。
p級數
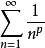 收斂級數
收斂級數p級數:
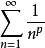 收斂級數
收斂級數(1)當 p>1 時,收斂;
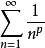 收斂級數
收斂級數(2)當 p ≤1時,發散。

