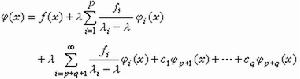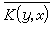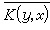相同,即
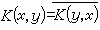，(x,y∈【α,b】)，則K(x,y)稱為對稱核，或埃爾米特核。具有對稱核的第二種弗雷德霍姆積分方程 稱為對稱核積分方程，或簡稱對稱方程。
(1)
對稱核的一切特徵值都是實的。不同的特徵值所對應的特徵函式是正交的。對稱核的特徵值是可列的。對應於每個特徵值的線性無關的特徵函式是有限的，因此，可就對應於同一個特徵值的最大個數的線性無關特徵函式進行正交標準化，從而，線性無關的特徵函式的全體構成一個正交標準的特徵函式序列。
為了方便，通常規定一個特徵值僅對應於一個特徵函式（若某一特徵值對應於n個線性無關的特徵函式,則視該特徵值有 n個）。於是可按特徵值的絕對值大小排列：
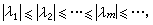
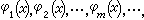(2)
D.希爾伯特和E.施密特證明了關於對稱方程的一個基本定理，即每個非零的對稱核至少有一個特徵值。設
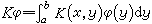,記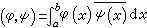
,則對稱核最小特徵值 λ1的絕對值的倒數等於(
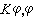)的絕對值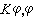｜()｜在條件(φ,φ)=1下的極大值，且當特徵函式φ1(x) 與最小特徵值 λ1對應時，有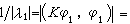
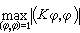。類似地,有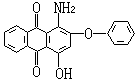
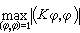，其中φ還同時滿足(φ,φm)=0，m=1，2,…,i-1。套用這個定理可以求特徵值的近似值，如常用的里斯方法即以此為根據。 設λ1，λ2…是對稱核K(x,y)的一切特徵值，φ1(x)，φ2(x)，…是相應的正交標準的特徵函式序列，h(x)是【α,b】上平方絕對可積的函式，而且積分
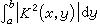關於x均勻有界，則函式 
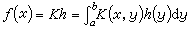可按正交標準的特徵函式序列 {φi(x)}展成為絕對一致收斂的級數： 
，
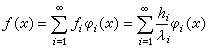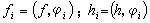。這就是著名的希爾伯特-施密特展開定理。 根據這個定理，可得到關於對稱核及其疊核的展開式:
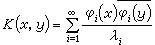，同時關於兩個變數是收斂和均值收斂的。
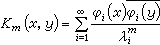，當m≥3時，它同時關於兩個變數x、y是絕對一致收斂的，而當m=2時,任固定一個變數則對另一個變數是絕對一致收斂的。 若對稱核K(x,y)是連續的，則有更好的結果，即梅瑟爾定理：設K(x,y)只有有限個正的或負的特徵值，則
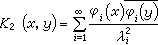同時關於兩個變數x、y是絕對一致收斂的。 令
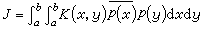。由希爾伯特-施密特展開定理可知，
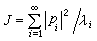。若對任意的平方絕對可積的函式p(x),恆有J≥0，則稱K(x,y)是正核;若J>0，則稱K(x,y)是正定核。否則使J≤0(J<0)的核稱為負核(負定核)。可以證明，對稱核為正（負）核的充分必要條件是它的一切特徵值都是正（負）的。對稱正(負)核為正定（負定）核的充分必要條件是核的特徵函式序列是完備的。 希爾伯特－施密特展開定理還可用來解非齊次對稱方程。若λ不是核 K(x,y)的特徵值;則非齊次方程(1)有惟一解φ(x), 且可表為
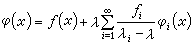，其中級數是絕對一致收斂的。若 λ是核K(x,y)的某個特徵值，即 λ=λp，它的秩為q，則非齊次方程 (1)若且唯若
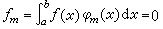,(m=p+1,p+2,…,p+q)滿足時才可解，且其解φ(x)可表為
