索伯列夫空間
正文
具有弱導數的多變數可積函式組成的一類巴拿赫空間。由於蘇聯數學家С.Л.索伯列夫對這類函式空間的發展作出了重要貢獻而以他的姓來命名。從30年代起,隨著變分法的發展和偏微分方程定解問題的解的存在性與正則性研究的需要,許多人研究了這類函式空間。索伯列夫空間及其各種推廣、嵌入定理、跡定理及各種插值公式已經成為偏微分方程理論必不可少的工具。設Ω是n維空間Rn中的一個區域。為了簡明起見,假定Ω是有界的。再設α=(α1,α2,…,αn)是非負整數組,|α|=α1+α2+…+αn,
 ,m為非負整數。下列函式集合賦以相應的範數都是巴拿赫空間:
,m為非負整數。下列函式集合賦以相應的範數都是巴拿赫空間: ① 捙上m階連續可微的函式的集合Cm(捙),其中的元素u的範數為
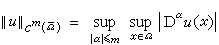 。
。 ② Cm(捙)中滿足赫爾德條件
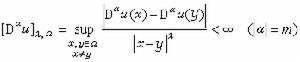
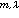 (捙)(0<λ≤1),u的範數為
(捙)(0<λ≤1),u的範數為 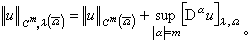
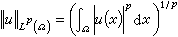 。
。 ④ 有界可測函式的集合L∞(Ω),元素u的範數為
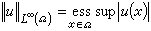 。
。
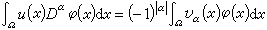
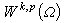 (或u∈
(或u∈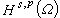 ),而函式υα稱為u的α階廣義導數或弱導數或分布導數,記為υα=Dαu。函式類
),而函式υα稱為u的α階廣義導數或弱導數或分布導數,記為υα=Dαu。函式類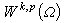 對範數
對範數 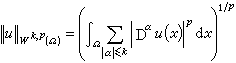
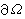 充分光滑時,空間
充分光滑時,空間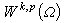 就是空間Ck(捙)關於範數(*)的完備化。W0 ,p(Ω)=Lp(Ω)。
就是空間Ck(捙)關於範數(*)的完備化。W0 ,p(Ω)=Lp(Ω)。 空間Hk(Ω)=W k,2(Ω)中賦以內積
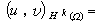
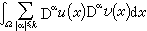 還成為希爾伯特空間。
還成為希爾伯特空間。 嵌入定理 設Ω
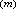 是含於捙的一個m維光滑流形;特別地,可以把Ω或Ω的子區域視為Ω
是含於捙的一個m維光滑流形;特別地,可以把Ω或Ω的子區域視為Ω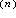 ,把
,把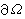 視為Ω(n-1)把m 維平面與捙的交視為Ω
視為Ω(n-1)把m 維平面與捙的交視為Ω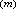 。
。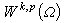 中的函式u可以視為Ω
中的函式u可以視為Ω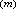 上定義的函式,稱為u在Ω
上定義的函式,稱為u在Ω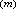 上的跡,記為
上的跡,記為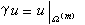 , 並稱у為把Ω上的函式映射為Ω
, 並稱у為把Ω上的函式映射為Ω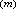 上的函式的跡運算元。當Ω
上的函式的跡運算元。當Ω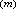 =Ω
=Ω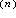 =Ω時,у為恆等運算元。
=Ω時,у為恆等運算元。 記X=
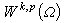 ,設Y為定義在Ω
,設Y為定義在Ω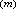 上的函式組成的一個巴拿赫空間。若u∈x則必有γu∈Y,且跡運算元γ是x到Y的有界運算元,就稱空間x嵌入空間Y,記為x戺Y。若嵌入運算元γ又是緊運算元,則稱x緊嵌入Y,記為x戺戺Y。
上的函式組成的一個巴拿赫空間。若u∈x則必有γu∈Y,且跡運算元γ是x到Y的有界運算元,就稱空間x嵌入空間Y,記為x戺Y。若嵌入運算元γ又是緊運算元,則稱x緊嵌入Y,記為x戺戺Y。 嵌入定理 設1≤p<∞,當Ω的邊界
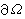 適當光滑時有以下結果。①當 m>n-pk≥0時,對
適當光滑時有以下結果。①當 m>n-pk≥0時,對 有
有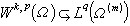 ;若
;若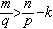 ,則
,則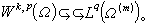 ②當
②當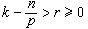 時,有
時,有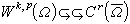 及
及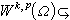
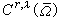 ,這裡,當
,這裡,當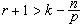 時,
時,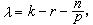 而當
而當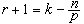 時,λ是(0,1)中的任意數。這個定理不能再改進了。例如,當
時,λ是(0,1)中的任意數。這個定理不能再改進了。例如,當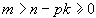 時,如果
時,如果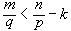 ,那么存在
,那么存在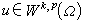 ,但
,但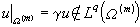 。
。 G.H.哈代與J.E.李特爾伍德在30年代初研究變分問題時建立的一些不等式實際上是對n=1的嵌入定理。上述的一般嵌入定理包含了許多人的工作。索伯列夫最初建立的嵌入定理只有:①當
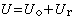 時,有
時,有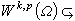
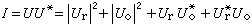 。②當
。②當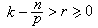 時,有
時,有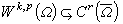 。緊嵌入
。緊嵌入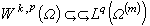 是 Л.Β.孔德拉紹夫證明的(1938)。嵌入
是 Л.Β.孔德拉紹夫證明的(1938)。嵌入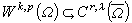 是 C.B.莫利證明的(1940)。
是 C.B.莫利證明的(1940)。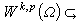
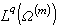 的極限指數
的極限指數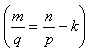 是Β.Л.伊利因證明的(1954)。把區域Ω的光滑性條件減到最弱(在情形①是所謂錐條件,在情形②是李普希茨條件)是E.加利亞爾多的工作(1958)。
是Β.Л.伊利因證明的(1954)。把區域Ω的光滑性條件減到最弱(在情形①是所謂錐條件,在情形②是李普希茨條件)是E.加利亞爾多的工作(1958)。 分數階空間與跡定理 當m =n-1時,對滿足上述嵌入定理的q,
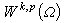 中的函式在
中的函式在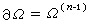 上的跡是Lq(
上的跡是Lq(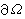 )中的函式;但是,並非所有Lq(
)中的函式;但是,並非所有Lq(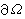 )中的函式都是空間
)中的函式都是空間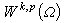 中某個函式在
中某個函式在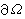 上的跡。然而,研究偏微分方程更加密切相關的問題是:定義在
上的跡。然而,研究偏微分方程更加密切相關的問題是:定義在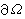 上的哪一類函式,其中每個函式都可以延拓到捙上而成為
上的哪一類函式,其中每個函式都可以延拓到捙上而成為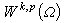 中的一個函式?為了解決這個問題,需要把空間
中的一個函式?為了解決這個問題,需要把空間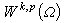 從整數k推廣到非整數s。從50年代起,許多人從不同途徑作了推廣工作。下面是常用到的分數階空間
從整數k推廣到非整數s。從50年代起,許多人從不同途徑作了推廣工作。下面是常用到的分數階空間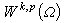 。
。 設s=m+σ,m為非負整數,0<σ<1。若u∈
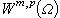 ,且u的所有m階弱導數都滿足條件
,且u的所有m階弱導數都滿足條件 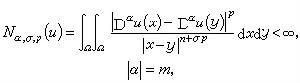
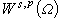 ,其範數定義為
,其範數定義為 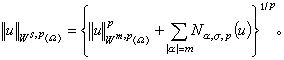
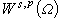 是巴拿赫空間。
是巴拿赫空間。 對上述問題的完整回答是跡定理:當邊界
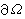 適當光滑時,對1<p<∞ 有
適當光滑時,對1<p<∞ 有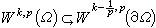 ,且嵌入運算元是滿映射(粗略地說,
,且嵌入運算元是滿映射(粗略地說,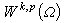 的函式在邊界
的函式在邊界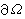 上失掉1/p階導數)。一般,命
上失掉1/p階導數)。一般,命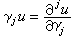 表示u在
表示u在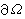 上的外法嚮導數,則跡運算元γ=(γ0,γ1,…,γk-1)是
上的外法嚮導數,則跡運算元γ=(γ0,γ1,…,γk-1)是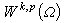 到
到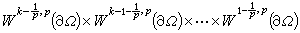 的滿映射。
的滿映射。 1951年,С.М.尼科利斯基研究了一類接近
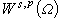 但稍大於
但稍大於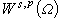 的空間
的空間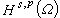 並建立了類似的跡定理。上述跡定理對p=2是由Л.Η.斯洛博傑茨基證明的(1958),對任意 p<1是經過加利亞爾多(1957)和С.Β.烏斯賓斯基(1960)先後研究完成的。J.-L.萊昂斯與E.馬格內斯通過內插空間理論研究空間
並建立了類似的跡定理。上述跡定理對p=2是由Л.Η.斯洛博傑茨基證明的(1958),對任意 p<1是經過加利亞爾多(1957)和С.Β.烏斯賓斯基(1960)先後研究完成的。J.-L.萊昂斯與E.馬格內斯通過內插空間理論研究空間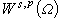 也得出了上述的跡定理(1961)。Ο.Β.別索夫於1959年開始研究另一類分數階空間
也得出了上述的跡定理(1961)。Ο.Β.別索夫於1959年開始研究另一類分數階空間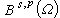 ,也證明相應的嵌入定理及跡定理。
,也證明相應的嵌入定理及跡定理。