定義
黎曼可積
 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式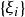 可積函式
可積函式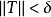 可積函式
可積函式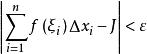 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式設 是定義在區間 上的一個函式, 是一個確定的實數。若對任意的正數 ,總存在某一正數 ,使得對 的任何分割 ,以及在其上任意選擇的點集 ,只要 ,就有 ,則稱 在區間 上可積或黎曼可積。
勒貝格積分
定義勒貝格積分常用的方法:
 可積函式
可積函式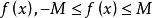 可積函式
可積函式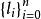 可積函式
可積函式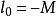 可積函式
可積函式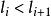 可積函式
可積函式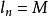 可積函式
可積函式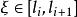 可積函式
可積函式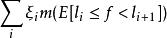 可積函式
可積函式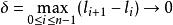 可積函式
可積函式對可測集 上的有界可測函式 ,找一串數 ,使 , , ,任取 ,討論和式 ,當 時,極限是否存在。
黎曼積分與勒貝格積分
黎曼積分在套用領域取得了巨大的成功,但是黎曼積分的套用範圍因為其定義的局限而受到限制。由於黎曼可積函式主要是連續函式或不連續點不太多的函式,使得黎曼積分在量子力學和機率論中的套用都遇到了瓶頸。僅從數學分析中的一些重要結果如積分與極限交換次序、重積分交換次序、牛頓一萊布尼茨公式等來看,黎曼積分要求的條件苛刻,對於一些問題的處理顯得力不從心,但是在勒貝格積分的框架下,上述問題就會得到較為圓滿的解決。另外為引入積分而得到的勒貝格測度概念還使數學分析中本來很難講清楚的一些道理(如單調函式的可微性、黎曼可積的充要條件等)變得清晰。
勒貝格積分是在勒貝格測度理論的基礎上建立起來的。這一積分可以統一處理函式有界與無界的情形,函式也可以定義在更一般的點集上,更重要的是它提供了比黎曼積分更廣泛有效的收斂定理。因此,勒貝格積分的套用領域更加廣泛,特別對機率論與數理統計的深入學習有十分重要的意義。
黎曼可積的各種條件
充分條件
 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式(1)設 在區間 上連續,則 在 上可積。
 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式(2)設 在區間 上有界,且只有有限個間斷點,則 在 上可積。
 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式(3)設 在區間 上單調有界,則 在 上可積。
必要條件
 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式定理:若函式 在 上可積,則 在 上必有界。
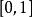 可積函式
可積函式該定理指出,任何一個可積函式一定是有界的,但是需要注意的是,有界函式不一定可積,如狄利克雷函式在 上有界但是不可積。
充要條件
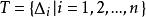 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式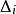 可積函式
可積函式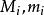 可積函式
可積函式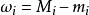 可積函式
可積函式 可積函式
可積函式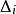 可積函式
可積函式設 為對 的任一分割。由 在 上有界,它在每個 上存在上、下確界,記為 ,設 ,稱為 在 上的振幅。
 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式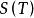 可積函式
可積函式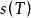 可積函式
可積函式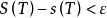 可積函式
可積函式定理1(可積準則):函式 在 上可積的充分必要條件是對任意的 ,總存在相應的一個分割 ,使得 關於分割 的上和 和下和 滿足 。
 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式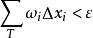 可積函式
可積函式定理2:函式 在 上可積的充分必要條件是對任意的 ,總存在相應的一個分割 ,使得 。
性質
函式乘積的可積性
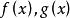 可積函式
可積函式 可積函式
可積函式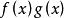 可積函式
可積函式設函式 在區間 上可積,那么乘積 也可積。
函式絕對值的可積性
 可積函式
可積函式 可積函式
可積函式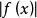 可積函式
可積函式如果函式 在區間 上可積,那么它的絕對值函式 也可積,並且滿足:
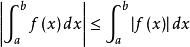 可積函式
可積函式積分值為正的條件
 可積函式
可積函式 可積函式
可積函式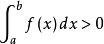 可積函式
可積函式(1)設函式 在區間 上恆正、可積,那么 。
 可積函式
可積函式 可積函式
可積函式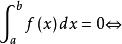 可積函式
可積函式 可積函式
可積函式 可積函式
可積函式(2)設函式 在區間 上非負、可積,那么 在區間 的每個閉子區間上 都有零點。
複合函式的可積性
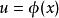 可積函式
可積函式 可積函式
可積函式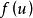 可積函式
可積函式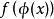 可積函式
可積函式 可積函式
可積函式設函式 在區間 可積,m 和 M 是它的上界和下界(m<M),函式 在 [m,M] 上連續,那么複合函式 在區間 可積。

