人物生平
 克卜勒
克卜勒 在圖賓根大學畢業後,克卜勒在格拉茨研究院當了幾年教授。在此期間完成了他的第一部天文學著作(1596年)。雖然克卜勒在該書中提出的學說完全錯誤,但卻從中非常清楚地顯露出他的數學才能和富有創見性的思想,於是偉大的天文學家第谷·布拉赫邀請他去布拉格附近的天文台給自己當助手。克卜勒接受了這一邀請,1600年1月加入了泰修的行列。第谷翌年去世。克卜勒在這幾個月來給人留下了非常美好的印象,不久聖羅馬皇帝魯道夫就委任他為接替第谷的皇家數學家。克卜勒在餘生一直就任此職。
作為第谷·布拉赫的接班人,克卜勒認真地研究了第谷多年對行星進行仔細觀察所做的大量記錄。第谷是望遠鏡發明以前的最後一位偉大的天文學家.
克卜勒認為通過對第谷的記錄做仔細的數學分析可以確定哪個行星運動學說正確的:哥白尼日心說,古老的托勒密地心說,或許是第谷本人提出的第三種學說。但是經過多年煞費苦心的數學計算,克卜勒發現第谷的觀察與這三種學說都不符合,他的希望破滅了。
最終克卜勒認識到了所存在的問題:他與第谷、拉格茨·哥白尼以及所有的經典天文學家一樣,都假定行星軌道是由圓或複合圓組成的。但是實際上行星軌道不是圓形而是橢圓形。
1600年,克卜勒出版了《夢遊》一書,這是一部純幻想作品,說的是人類與月亮人的交往。書中談到了許多不可思議的東西,像噴氣推進、零重力狀態、軌道慣性、宇宙服等等,人們至今不明白,近400年前的克卜勒,他是根據什麼想像出這些高科技成果的。儘管克卜勒的書是純幻想作品,但它一定有一些背景來源,比如像畢達哥拉斯的話或古希臘神話。
就在找到基本的解決辦法後,克卜勒仍不得不花費數月的時間來進行複雜而冗長的計算,以證實他的學說與第谷的觀察相符合。
克卜勒對此運動性質的研究,我們可以看到萬有引力定律已見雛形。克卜勒在萬有引力的證明中已經證到:如果行星的軌跡是圓形,則符合萬有引力定律。而如果軌道是橢圓形,克卜勒並未證明出來。牛頓後來用很複雜的微積分和幾何方法證出。
克卜勒除了發明行星運動定律外,還對天文學做出了許多小的貢獻。他也對光學做出了重要的貢獻。不幸的是他在晚年為私事而感到憂傷。當時德國開始陷入“三十年戰爭”的大混亂之中,很少有人能躲進世外桃源。
他遇到的一個問題是領取薪水。神聖羅馬皇帝即使在較興隆的時期都是怏怏不樂地支付薪水。在戰亂時期,克卜勒的薪水被一拖再拖,得不到及時的支付。克卜勒結過兩次婚,有十二個孩子,這樣的經濟困難的確很嚴重。另一個問題是他的母親在1620年由於行巫術而被捕。克卜勒花費了大量的時間設法使母親在不受拷打的情況下獲得釋放,他終於達到了目的。
克卜勒於1630年在巴伐利亞州雷根斯堡市去世。在“三十年戰爭”的動亂中,他的墳墓很快遭毀,但行星運行定律永存!
天才少年
克卜勒學業成績優異。1588年9月25日,他獲得文學學士學位。1591年8月11日,他又通過了文學碩士學位考試。這時他想當一名路德教的牧師,所以又留校學習神學。
在大學裡,克卜勒深受秘密傳播哥白尼學說的天文教授麥斯特林的影響。後來他回憶說:“當我在傑出的麥斯特林的指導下開始研究天文學時,看到了舊的宇宙理論的許多錯誤。我非常喜歡教授經常提到的哥白尼,在與同學們辯論時我總是堅持他的觀點。”克卜勒對天文學和數學有著濃厚的興趣。
1594年,奧地利的格拉茨新教高級中學的數學教師死了,要求圖賓根大學給選派一名後繼者。此時克卜勒的神學課程僅有一年就讀完了,但校方認為他作教士不夠虔誠,就極力推薦他去格拉茨。他的朋友也勸他放棄神學。同年克卜勒到了格拉茨中學教數學、天文,後來又教古典文學、修辭學和道德學。
1596年克卜勒在宇宙論方面發表了第一本重要的著作:《宇宙的神秘》。在其中他明確主張哥白尼體系,同時也因襲了畢達哥拉斯和柏拉圖用數來解釋宇宙構造的神秘主義理論。他在序言中指出:“我企圖去證明上帝在創造宇宙並且調節宇宙的次序時,看到了從畢達哥拉斯和柏拉圖時代起就為人們所熟知的五種正多面體,上帝按照這形體安排了天體的數目、它們的比例和它們運動間的關係。”他認為土星、木星、火星、地球、金星和水星的軌道分別在大小不等的六個球的球面上,六球依次套切成正四面體、正六面體、正八面體、正十二面體和正二十面體,太陽居中心。這種假設儘管荒唐,但卻促使克卜勒去進一步尋找正確的宇宙構造理論。他把這本書分寄給了一些科學名人。丹麥天文學家第谷·布拉赫雖不同意書中的日心說,卻十分佩服克卜勒的數學知識和創造天才。伽利略也把他引為探索真理的同仁。
由於反宗教改革運動,使格拉茨中學重新回到天主教的懷抱,新教徒的師生全被趕出了校門。克卜勒這位新教徒卻因名聲顯赫而被破例復聘。他看到自己的學生盡數散去,不願再回格拉茨,就接受了第谷的邀請,於1600年來到布拉格郊外的天文台,作第谷的助手。第谷是望遠鏡發明以前的最後一位偉大的天文學家,也是世界上前所未有的最仔細、最準確的觀察家。他當時充任神聖羅馬帝國的皇室數學家,隨皇帝魯道夫二世住在布拉格。他的宇宙理論是托勒密體系和哥白尼體系的混合,他認為行星繞太陽鏇轉,太陽又率群星圍地球運行。但是第谷對天體方位進行了幾十年的觀測,積累了大量的精確材料,克卜勒在天文學上的偉大發現,就是通過歸納分析這些材料得出的。
占星家
1601年第谷去世,克卜勒繼任為皇帝魯道夫二世的御用數學家。給他的俸祿只有第谷的一半,且常常拖欠。他對第谷的遺著作了整理,1602年出版了第谷的《新天文學》六卷,1603年印行了第谷的《釋彗星》。
1601年克卜勒出版了《天文學更可靠的基礎》一書,不同意星體決定人的命運的觀點,對占星術持懷疑態度:“如果星相家有時講對了,那應歸功於運氣。”但他仍沒擺脫宇宙的神秘和諧理論。除教數學外,他的一個主要任務就是替皇帝占星算命,這也是他終身從事的職業。在他的遺稿中保存了800多張占星圖。他雖不相信這一偽科學,但為了謀生只得如此。
立法者
 約翰內斯·克卜勒
約翰內斯·克卜勒 1604年9月30日,克卜勒在巨蛇星座附近發現了一顆新星(現知是銀河系內的一顆超新星)。他雖視力不佳,仍持續觀測了十幾個月。他把觀測結果發表在1607年出版的《巨蛇座底部的新星》一書中,打破了星座無變化的傳統說法。這一年他看到了一顆大彗星,即後來定名的哈雷彗星。
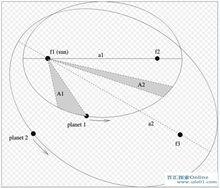
當時不論是地心說還是日心說,都認為行星作勻速圓周運動。但克卜勒發現,對火星的軌道來說,按照哥白尼、托勒密和第谷提供的三種不同方法,都不能推算出同第谷的觀測相吻合的結果,於是他放棄了火星作勻速圓周運動的觀念,並試圖用別的幾何圖形來解釋,經過四年的苦思冥想,也就是到了1609年他發現橢圓形完全適合這裡的要求,能做出同樣準確的解釋,於是得出了“克卜勒第一定律”:火星沿橢圓軌道繞太陽運行,太陽處於兩焦點之一的位置。發現第一定律,就是說行星沿橢圓軌道運動,需有擺脫傳統觀念的智慧和毅力,在此之前所有天文學家,包括哥白尼和伽利略在內都堅持古希臘亞里士多德和畢達哥拉斯的天體是完美的物體,圓是完美的形狀,一切天體運動都是圓周運動的成見。哥白尼知道幾個圓並起來可以產生橢圓,但他從來沒有用橢圓形來描述天體的軌道。當時由於第谷觀測的精確和克卜勒的努力,終使日心說向前推進了一大步。接著克卜勒又發現火星運行速度是不勻的,當它離太陽較近時運動得較快(近日點),離太陽遠時運動得較慢(遠日點),但從任何一點開始,向徑(太陽中心到行星中心的連線)在相等的時間所掃過的面積相等。這就是克卜勒第二定律(面積定律)。這兩條定律刊布在1609年出版的《新天文學》(又名《論火星的運動》)中,該書還指出兩定律同樣適用於其他行星和月球的運動。
1611年,克卜勒的保護人魯道夫被其弟逼迫退位,他仍被新皇帝留任。他不忍與故主分別,繼續隨侍左右。1612年魯道夫卒,克卜勒接受了奧地利的林茨當局的聘請,去作數學教師和地圖編制工作。在這裡他繼續探索各行星軌道之間的幾何關係,經過長期繁雜的計算和無數次失敗,最後創立了行星運動的第三定律(諧和定律):行星繞太陽公轉運動的周期的平方與它們橢圓軌道的半長軸的立方成正比。這一結果表述在1619年出版的《宇宙諧和論》中。
多難人生
克卜勒的身世是不幸的。他17歲時父親去世。1620年,他母親,一個酒館老闆的女兒,平時愛吵吵鬧鬧,因被指控犯有巫術罪而入獄,他經一年多的奔波才使其得到無罪釋放。克卜勒26歲時與一個出身名門的寡婦結婚,舉止傲慢的妻子使他很少感到家庭溫暖。1613年在前妻死後他又選擇了一個貧家女為伴,感情雖很融洽,無奈經濟上常處於絕望境地。他兩個妻子共生有12個小孩,大多在貧困中夭折。他作為新教徒常受到天主教會的迫害,他的一些著作被教皇列為禁書。
經濟困苦和操勞跋涉嚴重損害了克卜勒的健康。皇帝即使在較興隆的時期都是怏怏不樂地支付薪水。在戰亂時期,克卜勒的薪水被一拖再拖,得不到及時的支付。
1630年他有幾個月未得薪俸,不得不親自前往正在舉行帝國會議的雷根斯堡索取。到達那裡後他突然發熱,幾天以後即11月15日,在貧病交困中寂然死去,終年59歲。他被葬於拉提斯本的聖彼得教堂,三十年戰爭的狂潮蕩平了他的墳墓,但是也已證明他的行星運動定律是一座比任何石碑都更為久佇長存的紀念碑 。
魯道夫星表
 行星定律
行星定律 1618年三十年戰爭爆發,林茨為戰亂所擾,克卜勒受義大利波倫亞大學之聘任教三年(1618—1621)。此期間他發表了《哥白尼天文學概要》一書,闡發了哥白尼的理論,敘述了他個人對宇宙結構及大小的看法。該書論及日月食甚詳,記述1567年的日食為“四周有光環溢出,參差不齊”,由此可見這不是日環食,而是日冕現象。不久他又出版了《彗星論》一書,他認為彗星的尾所以總背著太陽,是由於太陽光排斥彗頭物質所致。這是提前兩個半世紀預言了輻射壓力的存在。
克卜勒晚年根據他的行星運動定律和第谷的觀測資料編制了一個行星表,為紀念他的保護人而定名為《魯道夫星表》。星表出版需大筆資金,雖然威尼斯共和國支付了其中的大部分,但籌集餘額仍給他帶來不少麻煩。後來皇家財政機關予以補助,星表才得以在1627年印行。這是他當時最受人欽佩的功績,由此表可以知道各行星的位置,其精確程度是空前的,直到十八世紀中葉它仍被視為天文學上的標準星表。1629年他出版了《1631年的稀奇天象》一書,預報了1631年11月7日水星凌日現象。至於他推算的金星凌日因發生在夜間,西歐看不到。在他的遺稿中尚有《新天文集》一書未及整理出版。
科學研究
天文研究
 約翰內斯·克卜勒
約翰內斯·克卜勒 在圖賓根大學畢業後,克卜勒在格拉茨研究院當了幾年教授。在此期間完成了他的第一部天文學著作(1596年)。雖然克卜勒在該書中提出的學說完全錯誤,但卻從中非常清楚地顯露出他的數學才能和富有創見性的思想,於是偉大的天文學家第谷·布拉赫邀請他去布拉格附近的天文台給自己當助手。克卜勒接受了這一邀請,1600年1月加入了第谷的行列。第谷翌年去世。克卜勒在這幾個月來給人留下了非常美好的印象,不久聖羅馬皇帝魯道夫就委任他為接替泰修的皇家數學家。克卜勒在餘生一直就任此職。
作為第谷·布拉赫的接班人,克卜勒認真地研究了第谷多年對行星進行仔細觀察所做的大量記錄。第谷是望遠鏡發明以前的最後一位偉大的天文學家,也是世界上前所未有的最仔細、最準確的觀察家,因此他的記錄具有十分重大的價值。克卜勒認為通過對第谷的記錄做仔細的數學分析可以確定哪個行星運動學說是正確的:哥白尼日心說,古老的托勒密地心說,或許是第谷本人提出的第三種學說。但是經過多年煞費苦心的數學計算,克卜勒發現第谷的觀察與這種三學說都不符合,他的希望破滅了。
他在1609年發表的偉大著作《新天文學》中提出了他的前兩個行星運動定律。行星運動第一定律認為每個行星都在一個橢圓形的軌道上繞太陽運轉,而太陽位於這個橢圓軌道的一個焦點上。行星運動第二定律認為行星運行離太陽越近則運行就越快,行星的速度以這樣的方式變化:行星與太陽之間的連線在等時間內掃過的面積相等。十年後克卜勒發表了他的行星運動第三定律:行星距離太陽越遠,它的運轉周期越長;運轉周期的平方與到太陽之間距離的立方成正比。
克卜勒定律對行星繞太陽運動做了一個基本完整、正確的描述,解決了天文學的一個基本問題。這個問題的答案曾使甚至像哥白尼、伽利略這樣的天才都感到迷惑不解。當時克卜勒沒能說明按其規律在軌道上運行的原因,到17世紀後期才由艾薩克·牛頓闡明清楚。牛頓曾說過:“如果說我比別人看得遠些的話,是因為我站在巨人的肩膀上。”克卜勒無疑是他所指的巨人之一。
光學研究
克卜勒也是近代光學的奠基者,他研究了針孔成像,並從幾何光學的角度加以解釋,並指出光的強度和光源的距離的平方成反比。克卜勒也研究過光的折射問題,1611年發表了《折光學》一書,最早提出了光線和光束的表示法,並闡述了近代望遠鏡理論,他把伽利略望遠鏡的凹透鏡目鏡改成小凸透鏡,這種望遠鏡被稱為克卜勒望遠鏡。
克卜勒也研究過人的視覺,認為人看見物體是因為物體所發出的光通過眼睛的水晶體投射在視網膜上,闡明了產生近視和遠視的成因。克卜勒還發現大氣折射的近似定律,最先認為大氣有重量,並且說明了月全食時月亮呈紅色是由於一部分太陽光被地球大氣折射後投射到月亮上而造成的。1630年11月,克卜勒在雷根斯堡發高熱,幾天后在貧病中去世,葬於當地的一家小教堂。他為自己撰寫的墓志銘是:“我曾測量天空,現在測量幽冥。靈魂飛向天國,肉體安息土中。”
學術經歷
找定目標
伽利略的望遠鏡為哥白尼體系提供的論據是令人信服的,但畢竟還是間接的,只有定性意義。因為人們“坐地觀天”,能夠直接觀察到的只是行星在恆星天球上垂直於視線方向的位移,而不是它們在空間的“真實”運動。要直接論證哥白尼體系,必須探求行星的“真實軌道”,並加以嚴格考證。
另外,哥白尼首創的日心體系還殘留著托勒玫體系的若干成分,沒有完全擺脫古希臘以來的傳統天文學思想的束縛,認為天體只能作勻速圓周運動和勻速圓周運動的疊加。因此,為了解釋行星運行中存在較小的不均勻性,仍然保留了托勒玫的一部分本輪和偏心圓的設計。哥白尼的日心宇宙理論無疑是正確的,但他的體系是有缺陷的,很快就被推翻了。
竟哥白尼事業之功、揭開行星運動之謎的是不朽的德國天文學家約翰·克卜勒。
克卜勒出生在德國南部的瓦爾城。他的一生顛沛流離,是在宗教鬥爭(天主教和新教)情勢中渡過的。克卜勒原是個新教徒,從學校畢業後,進入新教的神學院——圖賓根大學攻讀,本想將來當個神學者,但後來卻對數學和天文學發生濃厚興趣和愛好。
圖賓根大學的天文學教授米海爾·麥斯特林(1550年~1631年)是贊同哥白尼學說的。他在公開的教學中講授托勒玫體系,暗地裡卻對最親近的學生宣傳哥白尼體系。克卜勒是深受麥斯特林賞識的學生之一,他從這位老師那裡接受哥白尼學說後,就成為新學說的熱烈擁護者。他稱哥白尼是個天才橫溢的自由思想家,對日心體系予以很高評價。
克卜勒能言善辯,喜歡在各種集會上發表見解。因而引起學院領導機構——教會的警惕,認為克卜勒是個“危險”分子。學院畢業的學生都去當神甫,克卜勒則未獲許可。他只得移居奧地利,靠麥斯特林的一點幫助在格拉茨高等學校中擔任數學和天文學講師及編制當時盛行的占星曆書。
占星術是一門偽科學,克卜勒不信這一套。他不相信天上那些星辰的運行和地上人類生息的禍福命運會有什麼相干!他曾為從事此項工作自我解嘲說:“作為女兒的占星術若不為天文學母親掙麵包,母親便要挨餓了。”
從那時起,克卜勒開始從事研究他畢生最感興趣,也是他爾後獲得最大成就的問題了。
宇宙模型
克卜勒平生愛好數學。他也和古希臘學者們一樣,十分重視數學的作用,總想在自然界尋找數字的規律性(早期希臘學者稱為"constant")。規律愈簡單,從數學上看就愈好,因而在他看來就愈接近自然。他之所以信奉哥白尼學說,正是由於日心體系在數學上顯得更簡單更和諧。他說:“我從靈魂深處證明它是真實的,我以難以相信的歡樂心情去欣賞它的美。”他接受哥白尼體系後就專心探求隱藏在行星中的數量關係。他深信上帝是依照完美的數學原則創造世界的。
克卜勒在他早期所著的《神秘的宇宙》(1597年)一書里設計一個有趣的、由許多有規則的幾何形體構成的宇宙模型。克卜勒試圖解釋為什麼行星的數目恰好是六顆,並用數學描述所觀測到的各個行星軌道大小之間的關係。他發現六個行星的軌道恰好同五種有規則的正多面體相聯繫。這些不同的幾何形體,一個套一個,每個都按照某種神聖的和深奧的原則確定一個軌道的大小。若土星軌道在一個正六面體的外接球上,木星軌道便在這個正六面體的內切球上;確定木星軌道的球內接一個正四面體,火星軌道便在這個正四面體的內切球上;火星軌道所在的球再內接一個正十二面體,便可確定地球軌道……照此交替內接(或內切)的步驟,確定地球軌道的球內接一個正二十面體,這個正二十面體的內切球決定金星軌道的大小;在金星軌道所在的球內接一個正八面體,水星軌道便落在這個正八面體的內切球上。
克卜勒也因循自亞里士多德、托勒密直至哥白尼以來的固有見解,沒有跳出圓形軌道的框框。
這種設計得到的各個球的半徑比率與各個行星軌道大小的已知值相當吻合。有規則的正多面體是具有相同平面的對稱體。這種具有對稱平面的多面體只能作出五個,因此克卜勒確信太陽系的行星只有六顆。
 偉大的克卜勒
偉大的克卜勒 這一“發現”給克卜勒帶來極大喜悅,他寫道:“我從這個發現所得到的極度喜悅是無法用語言來表達的。我不怕任何麻煩,我不辭辛勞、日以繼夜地進行計算,直到我能夠看到是否我的假設符合哥白尼的軌道,或者是否我的喜悅要落空”。
克卜勒模型的數學關係縱然如此美妙,但若干年後克卜勒分析第谷的觀測數據、制定行星運行表時,它們卻毫無用處。克卜勒就摒棄了它。
1598年奧地利暴發宗教衝突。天主教徒用兇殘的懲罰來恫嚇克卜勒。他被迫離開奧地利,逃到匈牙利隱蔽起來。不久,他接到在布拉格路德福國王宮廷內任職的第谷的邀請,去協助整理觀測資料和編制新星表。克卜勒欣然接受,1600年攜眷來到布拉格,任第谷的助手。
具有諷刺意味的是,這兩位學者,一個始終是哥白尼體系的反對者,另一個則是該體系的衷心擁護者。但他們畢竟撮合在一起了,並且戲劇般地成為天文學史上合作的光輝典範!
這是克卜勒最快樂的時代,他不再為生活而發愁,專心從事天文學研究。然而很不幸,他們相處沒有多久,第谷便於第二年(1601年)去世。克卜勒遭到一次很沉重的打擊。這位被稱為“星學之王”的天文觀測家把他畢生積累的大量精確的觀測資料全部留給了克卜勒。他生前曾多次告誡克卜勒:一定要尊重觀測事實!
克卜勒繼任第谷的工作,任務是編制一張同第谷記錄中的成千個數據相協調的行星運行表。雖然他得到“皇家數理家”的頭銜,但宮廷卻不發給他應得俸祿,他不得不再從事星相術來餬口。
第谷的觀測記錄到了克卜勒手中,竟發揮意想不到的驚人作用,使克卜勒的工作變得嚴肅起來。他發現自己的得意傑作——克卜勒宇宙模型,在分析第谷的觀測數據、制訂行星運行表時毫無用處,不得不把它摒棄。不論是哥白尼體系、托勒玫體系還是第谷體系,沒有一個能與第谷的精確觀測相符合。這就使他決心查明理論與觀測不一致的原因,全力揭開行星運動之謎。為此,克卜勒決定把天體空間當做實際空間來研究,用觀測手段探求行星的“真實”軌道。
巧奪天工
克卜勒要解決的問題包括兩方面:第一,用什麼方法測定行星(包括地球)運動的“真實”軌道,如同觀測者能從“天外”看行星繞太陽運行一樣;第二,分析行星運動遵循什麼樣的數學定律。
如今已很少有人想到,克卜勒如何從行星的使人眼花繚亂的視行中推出它們的“真實”軌道?只要想到人們永遠不可能看到行星的真實運動,而只能從運動著的地球上看到它們在天空的什麼方向,就知道問題困難了。倘使行星所作的是簡單的勻速圓周運動,從地球上看去,還比較容易地察覺這種運動該是怎樣的;可是實際情形比這要複雜得多,而且地球本身同樣是以某種未知方式繞太陽運動。這就使問題變得無比複雜和困難了。
克卜勒用一個絕妙方法把這種雜亂無章的現象理出一個完整清楚的頭緒來。他同哥白尼一樣,敏銳地領悟到,“要研究天,最好先懂得地”,他也把著眼點放在地球上,力圖先摸清地球本身的運動,然後再研究行星的運動。
但是這樣做的時候,並沒有排除行星存在的必要性。假如天空中只有太陽和恆星而沒有別的行星存在,那要找出地球的“真實”軌道,還是辦不到的。因為在那種情形下,除了太陽的周年視行外,其他就沒有什麼東西可以從經驗上來確定。它雖然也能幫助我們確定地球繞太陽運行的方式,譬如地球向徑(日地連線)在一個相對恆星是靜止的平面(黃道面)上運動,這種運動的角速度在一年中呈現有規律的變化……。但是,光知道這些並沒有多大用處,關鍵是必須確定地球同太陽之間的距離在一年中是怎樣變化的?只有當人們弄清這種變化後,才能確定地球軌道的真實形狀及它的運行方式。
其實,克卜勒所用的方法就是普通的三角測量法。
在大地測量工作中,常常要測定那些由於某種自然障礙而無法直接到達的目標的距離。假定需要測定A地到對岸塔C的距離,因A、C兩地被大河阻隔,無法直接去測量這段距離的長度。為了解決這個困難,觀測者可在河的這岸另擇一點B,AB的距離是可以直接丈量的。這段經過選定的、已知其長度的線段AB,用測量學的術語來說,叫做“基線”。基線確定後,可在它的兩端用測角儀分別測定A、B兩角的大小。於是,在三角形ABC中,已知兩角大小和它們所夾的邊(基線)長,三角形的其他角和邊,就可以計算出來。套用這個簡單方法可以求得無法達到的目標的距離。
實際上,天文學家們也是用這個方法來測定天體距離的。只不過這個問題對天文學家說來更加困難些,因為天文學家們要布設一條“基線”不那么容易。克卜勒所遇到的正是這個困難。
克卜勒要測定地球(在其軌道上)與太陽的距離。在這裡,太陽好比是上述例證中的A地,地球則是河對岸的那座塔C。為了布設“基線”,還需要另找一個定點B。可是,在行星系統里,除了太陽是唯一“靜止”的中心天體外,再也找不出第二個這樣的“定點”。這要由克卜勒另行覓取。
我們構想在地球軌道平面的某處有一盞明亮的天燈M,它有足夠的明亮度,並且永遠懸掛在那裡,以使地球上的觀測者在每年任何日期都能看到它;又假定這燈距太陽比地球還要遠些。如果具備這些條件,它就成了我們所需要的第個定點。太陽與燈的連線就是我們所要布設的“基線”。藉助這樣一盞燈,就能用下述辦法來測定地球的軌道。
譬如,每年都會有這樣一個時刻,地球(E)正好在太陽(S)和燈(M)的連線上。這時,從地球上來看燈,我們的視線EM就會同SM(太陽~燈)重合,我們可以把後者在天空中的位置(它指向某一恆星)記錄下來。
以後,在另一個時刻,地球運行到軌道上的另一位置E',這時它同太陽和那盞燈的位置形成一個三角形SE'M。
在這個三角形中,SM邊是事先選定的“基線”;e角的大小可以從地球上同時觀測太陽和燈M來確定;S角就是地球向徑(SE")同基線SM所夾的角,其大小也可以通過對恆星的觀測來確定。有了這些已知條件,便可以得知三角形SE'M中SE"的距離,或者說地球E'相對於基線SM的位置完全可確定。
因此,只要在紙上任意畫一條基線SM,憑著我們觀測到的e和S的角度,就可以作出三角形SE'M來。我們可以在一年中經常這樣做,每次都會在紙上得到地球E'對於那條基線SM的不同位置,並且給它們逐個註上日期,然後把這些點連成曲線……。這樣,我們就從經驗上確定了地球的軌道。雖然其大小還是相對的,然而卻是“真實”的。
可是從哪裡去找這盞燈呢?要知道行星系統里除了中心天體——太陽外,所有能看得見的客體都不是靜止的,它們的運動在細節上都是未知的。克卜勒毫不費事地找到這盞燈。它就是火星,一盞天上的“紅燈”。
人們不禁要問:火星不也是在運動嗎?
一點不錯,火星確是在運動。然而聰明的克卜勒想出一條“動中取靜”的妙計。那時人們對火星的視運動已經知道得非常清楚,它繞太陽運行的周期(一個“火星年”)是精密地測定了的。既然它是在閉合的軌道上運行,就總會有這么一個時刻,即太陽、地球和火星處在同一直線上,而且每隔一個“火星年”之後,它總又要回到天空的同一位置上來。因此,火星雖然是動的,但在某些特定的時刻,SM總是表現為同一條基線;而地球呢?在這些時刻,它會到達自己的不同位置。這時,對太陽和火星同時進行觀測,就成為克卜勒測定地球軌道的手段;火星這時就起著所構想的那盞燈的作用。
“天公鬥巧乃如此,令人一步千徘徊”。克卜勒就是這樣以令人讚嘆的巧妙手法把地球軌道的形狀測了出來。地球的軌道一經測定,地球及其向徑
(SE)在任何時刻的實際位置和距離變化,也就成為已知條件。反過來,以地球向徑作為基線,從觀測數據中推求其他行星的軌道和運動,對克卜勒來說不再是太困難的事了!
8分誤差改變整個天文學
行星軌道從經驗中算出來了,下一步要弄清楚的問題是行星運動究竟遵循什麼數學定律?
乍看,第一個問題解決後,搞清楚第二個問題該是輕而易舉的事。然而你馬上就會看到,要從經驗的數據里推出運動定律要比解決第一個問題艱巨得多。
克卜勒首先需要了解行星軌道所描出的曲線的幾何特徵是什麼?為此,他必須先作某種假設,然後把它用到一大堆數字上去試試,看它是否能同第谷的數據吻合。如果不是,再找另外的假設進行探索,直到合乎觀測事實為止。
克卜勒的目光首先盯住火星。這是因為第谷的數據中對火星的觀測占有最大篇幅。恰好,就是這個行星的運行與哥白尼理論出入最大。克卜勒按照傳統的偏心圓來探求火星的軌道。他作了大量嘗試,每次都要進行艱巨的計算。在大約進行了70次的試探之後,克卜勒才算找到一個與事實相當符合的方案。使他感到驚愕的是,當超出他所用數據的範圍繼續試探時,他又發現與第谷的其他數據不符。火星還是不聽他的擺布……。
克卜勒詼諧地寫道:“我預備征服戰神馬爾斯,把它俘虜到我的星表中來,我已為它準備了枷鎖。但是我忽然感到勝利毫無把握……,這個星空中狡黠的傢伙,出乎意料地扯斷我給它戴上的用方程連成的枷鎖,從星表的囚籠中衝出來,逃往自由的宇宙空間去了。”
克卜勒計算出來的火星位置和第谷數據之間相差8分,即1.133度(這個角度相當於表上的秒針在0.02秒瞬間轉過的角度)會不會是第谷弄錯了呢?或是寒冷的冬夜把第谷的手指凍僵了,以致觀測失誤了呢?不會!克卜勒完全信賴第谷觀測的辛勤與精密,即使是這樣微小的數值,第谷也是不會弄錯的。他說:“上天給我們一位像第谷這樣精通的觀測者,應該感謝神靈的這個恩賜。一經認識這是我們使用的假說上的錯誤,便應竭盡全力去發現天體運動的真正規律,這8分是不允許忽略的,它使我走上改革整個天文學的道路。”可見,這兩位天文學大師的工作在當時已達到何等驚人的精確性!
當克卜勒意識到始終無法找出一個符合第谷觀測數據的圓形軌道後,他就大膽摒棄這種古老的、曾寄希望的勻速圓周運動的偏見,嘗試用別的幾何曲線來表示所觀測到的火星的運動。克卜勒認為行星運動的焦點應在施引力的中心天體——太陽的中心。從這點出發,他斷定火星運動的線速度是變化的,而這種變化應當與太陽的距離有關:當火星在軌道上接近太陽時,速度最快;遠離太陽時,速度最慢。他並且認為火星在軌道上速度最快與最慢的兩點,其向徑圍繞太陽在一天內所掃過的面積是相等的。然後,他又將這兩點外面積的相等性椎廣到軌道上所有的點上。這樣便得出面積與時間成正比的定律。
隨後,克卜勒看出火星的軌道有點像卵形(幸運的是,他首先選中火星,而火星軌道的偏心率在行星中比起來是相當大的),在連線極大與極小速度兩點方向的直徑似乎伸得長些。這樣,終於使他認識到火星是在橢圓的軌道上運動。
橢圓是人們比較熟悉的幾何圖形。我們可以從木工師傅那裡學到它的機械畫法:在木板上先定出兩個點,釘上釘子,取一段定長而無伸縮性的線,把它的兩端固定在釘子上,用鉛筆套在裡面,然後把線拉緊,慢慢移動鉛筆,這樣畫出來的曲線便是一個橢圓。
這個畫法告訴我們,橢圓上的任何一點到兩個定點的距離之和保持不變。它的數學定義便是:若平面上動點到兩定點的距離之和是常量,動點的軌跡叫做橢圓。兩個定點叫做橢圓的焦點,焦點之間的距離叫做焦距。
橢圓的變化情形可用偏心率e來表示。橢圓的偏心率是它的焦距與它的長徑的比率,e通常是用下式來表示的。
c
e=(c是半焦距,a是半長徑)
a
∵c可以看出,焦距越大,e的值越接近於1,橢圓形狀越扁;反之,焦距越小,e的值越接近於零,橢圓形狀越變渾圓;當焦距為零,偏心率e=0時,橢圓也就轉化為圓。從這個意義上說,可以把圓看作是橢圓的一種特殊情形,即兩個焦點重合的橢圓。
太陽系各個行星軌道的具體形狀稍有不同。一般說來,它們的偏心率都很小,同圓形只有微小的差異。所以行星軌道可以近似地看作圓形,太陽的位置也可以近似地看作位於軌道的中心。這便是當年使克卜勒絞盡腦汁的原因。
這一回又是幾何學幫了天文學的大忙。假使沒有古希臘人對圓錐曲線(平面截割圓錐所形成的曲線)的研究,這些美妙的定律也許不可能被發現。由於橢圓是圓錐曲線的一種,它那種圓而帶扁的形狀使克卜勒想到火星可能在這樣一種曲線的軌道上運動。跟著,利用古代幾何學家對圓錐曲線尋找出來的許多性質,他肯定自己所作的假設是正確的,並將這兩項發現推廣到所有行星。
1609年,克卜勒發表了《新天文學》一書和《論火星運動》一文,公布了兩個定律:
(一)所有行星分別在大小不同的橢圓軌道上運動。太陽的位置不在軌道中心,而在軌道的兩個焦點之一。
這是行星運動第一定律(也叫軌道定律)。
(二)在同樣的時間裡,行星向徑在其軌道平面上所掃過的面積相等。
這是行星運動的第二定律(也叫面積定律)。
克卜勒雖然摒棄行星等速度運動的偏見,但仍維護這一原則,只是把線速度相等換了個“面速度”相等。這使克卜勒感到分外高興。有了這個定律,可以計算任何時刻行星在軌道上的位置。
這兩個重要的定律相繼發現後,編制星表一事便輕而易舉了。不僅“行蹤詭秘”的火星永遠逃不出星表的“囚籠”,馴服地沿克卜勒給定的橢圓軌道運行,其餘各個行星也都相繼“被俘”。
奇妙的“2”和“3”
克卜勒並不滿足已取得的成就,他感到自己遠遠沒有揭開行星運動的全部奧秘。他相信還存在著一個把全部行星系統連成一個整體的完整定律。
古人給了他啟示,行星運行的快慢同它們的軌道位置有關,較遠的行星有較長的運行周期。第二定律也表明,即使在同一軌道上,行星速度也因距太陽遠近而變化。沿著這條思路,克卜勒確信行星運動周期與它們軌道大小之間應該是“和諧”的。他要找出其間的數量關係來。
克卜勒是怎樣尋找這個關係的呢?他面對的只是一些觀測數據,要在它們背後找出隱藏著的自然規律來,這就要求這位天文學家具有高度驚人的毅力和耐心。
克卜勒和哥白尼一樣,並不知道行星與太陽之間的實際距離,只知道它們距太陽的相對遠近。他把地球作為比較標準:以日地平均距離(天文單位)為距離單位;以地球繞太陽運動周期(一年)為時間單位。把各個行星的公轉周期 (T)及它們與太陽的平均距離(R)排列成一個表,以探討它們之間存在什麼數量關係。
行星名稱 公轉周期 (T) 太陽距離 (R)
水星 0.241 0.387
金星 0.615 0.723
地球 1.000 1.000
火星 1.881 1.524
木星 11.862 5.203
土星 29.457 9.539
從這個表中可知,對水星而言,公轉周期是0.241年,距離是0.387天文單位;而對金星來說,則分別為0.615年和0.723天文單位……余類推。這么一堆亂七八糟的數字能反映出什麼規律性呢?像做數字遊戲一樣,克卜勒對表中各項數字翻來覆去作各式各樣的運算:把它們互相乘、除、加、減;又把它們自乘;時而又求它們的方根……這樣,在很少有人了解和支持的困難情況下,他頑強地苦戰達9年之久。經過無數次的失敗,他終於找到一個奇妙的規律。他在原來的那個表里增添兩列數字:
2 3
行星名稱 公轉周期 (T) 太陽距離 (R)周期平方 (T)距離立方 (R)
水星 0.241 0.387 0.058 0.058
金星 0.615 0.723 0.378 0.378
地球 1.000 1.000 1.000 1.000
火星 1.881 1.524 3.54 3.54
木星 11.862 5.203 140.7 140.85
土星 29.457 9.539 867.7 867.98
從這個表的後面兩列數字里,我們可以看出這個奇妙的規律:行星公轉周期的平方與它同太陽距離的立方成正比。
即:
T2(T的平方)=R3(R的立方)
這就是行星運動的第三定律(也叫周期定律)。
由此可知,行星同太陽的距離,可以根據該行星公轉的恆星周期來計算,即:
R2(R的平方)=T2(T的平方)
這個謎一經猜破,似乎十分簡單。但在謎底揭開之前,它著實叫克卜勒耗盡心血。這對奇妙的“2”和“3”得來並非容易!
克卜勒在獲得這一成就時喜不自禁的寫道:“……(這正是)我十六年以前就強烈希望要探求的東西。我就是為這個而同第谷合作……現在我終於揭示出它的真相。認識到這一真理,這是超出我的最美好的期望。大事告成,書已寫出來了,可能當代就有人讀它,也可能後世才有人讀,甚至可能要等待一個世紀才有讀者,就像上帝等了六千年才有信奉者一樣。這我就管不著了”。他寫得多么得意呀!
如果克卜勒當時能知道對數運算的話,問題就要簡單得多。若取表中各個行星的周期(T)和距離(R)的對數(見下表右邊兩欄列出的數字)進行比較:
行星名稱 周期 (T) 距離 (R) lgT lgR
水星 0.241 0.387 0.62 0.41
金星 0.615 0.723 0.21 0.14
地球 1.000 1.000 0 0
火星 1.881 1.524 0.27 0.18
木星 11.862 5.203 1.07 0.72
土星 29.457 9.539 1.47 0.98
那就用不著克卜勒那樣高超的智慧,任何人都會立即看出:
lgT∶lgR=3∶2
這是一個十分重要的自然定律。不僅行星遵循著它,連同行星的衛星以及太陽周圍的其他天體概無例外。從而可以確定,太陽和它周圍的所有天體不是偶然的、沒有秩序的“烏合之眾”,而是一個有嚴密組織的天體系統——太陽系。
給天空立法
為紀念克卜勒在天文學上的卓著功績,上述行星運動三大定律,被稱“克卜勒定律”。它一經確立,本輪系徹底垮台,行星的複雜運動,立刻就失去全部神秘性。它成了天空世界的“法律”。後世學者尊稱克卜勒為“天空立法者”。
不知是什麼原因,克卜勒的這些重大發現卻沒有引起與他同時代的伽利略的足夠重視。兩人畢生都為哥白尼學說而奮鬥,他們又是朋友,時有書信往來,然而對於克卜勒的這一決定性的進展,伽利略一生和著作中竟沒有留下任何痕跡。這也是科學史上的一樁怪事!
克卜勒定律在天文學上有十分重大的意義:
首先,克卜勒定律在科學思想上表現出無比勇敢的創造精神。遠在哥白尼創立日心宇宙體系之前,許多學者對於天動地靜的觀念就提出過不同見解。但對天體遵循完美的均勻圓周運動這一觀念,從未有人敢懷疑。克卜勒卻毅然否定了它。這是個非常大膽的創見。哥白尼知道幾個圓合併起來就可以產生橢圓,但他從來沒有用橢圓來描述過天體的軌道。正如克卜勒所說,
“哥白尼沒有覺察到他伸手可得的財富”。
其次,克卜勒定律徹底摧毀了托勒玫的本輪系,把哥白尼體系從本輪的桎梏下解放出來,為它帶來充分的完整和嚴謹。哥白尼拋棄古希臘人的一個先入之見,即天與地的本質差別,獲得一個簡單得多的體系。但它仍須用三十幾個圓周來解釋天體的表觀運動。克卜勒卻找到最簡單的世界體系,只用七個橢圓說就全部解決了。從此,不需再藉助任何本輪和偏心圓就能簡單而精確地推算行星的運動。
第三,克卜勒定律使人們對行星運動的認識得到明晰概念。它證明行星世界是一個勻稱的(即克卜勒所說的“和諧”)系統。這個系統的中心天體是太陽,受來自太陽的某種統一力量所支配。太陽位於每個行星軌道的焦點之一。行星公轉周期決定於各個行星與太陽的距離,與質量無關。而在哥白尼體系中,太陽雖然居於宇宙“中心”,卻並不扮演這個角色,因為沒有一個行星的軌道中心是同太陽相重合的。
由於利用前人進行的科學實驗和記錄下來的數據而作出科學發現,在科學史上是不少的。但像行星運動定律的發現那樣,從第谷的20餘年辛勤觀測到克卜勒長期的精心推算,道路如此艱難,成果如此輝煌的科學合作,則是罕見的。這一切都是在沒有望遠鏡的條件下得到的!
除了發現行星運動定律外,克卜勒在天文學上還作出有益的貢獻。他沒有辜負第谷的囑託,於1627年刊布他終身的最後傑作——《路德福星表》。這是天文史上值得稱讚的一部星表,它的完備和準確度遠勝過前人。在以後的百餘年間,該表一直被天文學家和航海家們奉為至寶。它的形式幾乎沒有改變地保留到如今。我們可從《天文年曆》或同類書刊中查知天體過去或未來的運動和準確位置。克卜勒正是這方面工作的先驅。
克卜勒自幼就損壞視力,沒能成為一位天文觀測家。他是“借別人的眼睛”作出自己的科學發現。可是他在光學理論和光學儀器研究方面卻作過重大貢獻。伽利略雖在望遠鏡的操作上有所改進,但他的望遠鏡原則上同荷蘭眼鏡匠製造的沒有什麼兩樣,由一塊凸鏡片(物鏡)和一塊凹鏡片(目鏡)合成。克卜勒(比伽利略稍晚些)則設計出一種新型望遠鏡。他把伽利略式望遠鏡的凹鏡片目鏡改用一個小凸透鏡,把長焦距的透鏡和短焦距的透鏡配合在一起,這好比給放大鏡“戴上一付眼鏡”,其倍率按物鏡和目鏡的焦距之比來決定。所成的像則是倒立的,這對天文學家來說,沒有什麼不方便。克卜勒式望遠鏡的特點是把目標放在兩透鏡的公共焦點上,能夠測定微小角度。它後來被廣泛套用於天文望遠鏡。
如同伽利略奠定實驗力學的基礎一樣,克卜勒則奠定了近代實驗光學的基礎。他看到光從已知光源以球面輻射出來,直覺地提出了光度隨距離減弱的平方反比定律。
這樣一位為科學發展開拓道路的勇士,一生卻是在極端艱難的條件下度過的。連年的戰爭,長期漂泊,生活貧困以及來自教會的迫害,不斷困擾著他。在他花甲之年,為向宮廷索取20餘年的欠薪,他長途跋涉去拉提明,於公元1630年11月15日染傷寒死在途中,只留下幾件衣服和一些書籍。
其他貢獻
克卜勒在物理學特別是光學領域作出了傑出貢獻。1604年他的《對威蒂略的補充,天文光學說明》一書問世。威蒂略(1220—1270)是中世紀著名的波蘭物理學家,著有《物理學》、《光學》等書,闡述了文藝復興以前最重要的光學理論。克卜勒在此基礎上又作了發展,他描述了人的視覺的形成過程,揭示了視網膜的作用,指明了近視和遠視的原因。雖然早在1299年佛羅倫斯的阿瑪蒂就發明了矯正視力的眼鏡,但直到克卜勒才解釋了這些彎曲的小玻璃片的作用。他對視覺的分析,給了解眼器官的結構和機能打下了基礎。
1609年克卜勒發表了《天文學中的光學》一書。同年伽利略發明了一架折射望遠鏡。伽利略望遠鏡由一塊凸鏡作物鏡和一塊凹鏡作目鏡組成,它成正像,但出射光瞳在目鏡與物鏡之間,視場小且不易安裝瞄準叉絲,在天文觀測中用途不大。克卜勒深入研究並闡釋瞭望遠鏡的原理,對摺射望遠鏡作了重大改進,設計了克卜勒望遠鏡。他以凸透鏡作目鏡,使出射光瞳在目鏡外面,能獲得較大視場,也可方便地安置瞄準叉絲。1613年製造出第一架克卜勒望遠鏡,至十七世紀中葉已為天文學家普遍採用。克卜勒關於望遠鏡的理論,寫在1611年出版的《光學》一書中。
克卜勒在說明望遠鏡原理時,看到光從已知光源以球面輻射出來,直覺地提出了光度隨距離減弱的平方的反比律,他覺得介質的折射力與介質的密度成正比,但是英國數學家哈略特向他指出,油比水的折射力大,但是油比水的密度小。正確的光的折射律是由萊頓的一位數學教授威里布里德·斯涅耳(1591—1626)於公元1621年發現的。
克卜勒最先認為大氣有重量,並正確解釋了月全食時月亮呈紅色是因太陽光經過大氣折射後投射到上面而造成的。他首先把潮汐同月球的活動聯繫起來,第一次宣布地球以外的行星也是物質的、不完美的。這是一個了不起的發現,但不知什麼原因,他的朋友伽利略卻不接受他關於潮汐的理論。
1611年克卜勒即興寫了一本未完成的書:《六角形的雪》。通過對六角的雪的觀察使他得出了對稱的觀念,並推想到雪是由許多球體緊密堆積而成。這本書可視為晶體學的發軔。
克卜勒在幾何學中也有獨到的建樹。1615年他發表了《葡萄酒桶的立體幾何》,這本書被稱為人類創造球面、體積新方法的靈感源泉。在這本書中,克卜勒用無窮大和無窮小的概念來代替古老而煩瑣的窮竭法,他構想一個由無數個三角形構成的圓,其中每個三角形的頂點都處在圓心,圓周是由它們無窮小的底邊構成。同樣,圓錐體可以看成是由大量具有共同頂點的稜錐體所構成,圓柱體是由大量稜柱體所構成,這些稜柱體的底邊構成圓柱體的底邊,它們的高就是圓柱體的高。克卜勒採用這些觀念得出了一些古人辛辛苦苦極難得到的結果。他的方法中雖缺少關於極限的明確概念,和有效的求和方法,但可導致正確的結果,他的方法給數學家開闢了一個廣闊的思考園地。
偉大遺產
克卜勒是近代自然科學的開創者之一。在天文學方面如果沒有他,日心說的命運當時將是不確定的。他的三大定律奠定了經典天文學的基石,為牛頓數十年後發現萬有引力定律鋪平了道路。他在科學研究中 一貫堅持尊重事實的嚴肅態度,當他發現構想與事實不符時,就毫不猶豫地拋棄了它們。但他畢竟是中世紀與近代交替時期的人物,思想上必然帶有時代的局限性。
克卜勒對天文學的貢獻幾乎可以和哥白尼相媲美。事實上從某些方面來看,克卜勒的成就甚至給人留下了更深刻的印象。他更富於創新精神。他所面臨的數學困難相當巨大。數學在當時遠不如今天這樣發達,沒有計算機來減輕克卜勒的計算負擔。
從克卜勒取得的成果的重要性來看,令人感到驚奇的是他的成果起初差一點被忽略,甚至差點被伽利略這樣如此偉大的科學家所忽略(伽利略對克卜勒定律的忽視特別令人感到驚奇,因為他倆之間有書信往來,而且克卜勒的成果會有助於伽利略駁斥托勒密學說)。如果說其他人遲遲不能賞識克卜勒成果的重大意義的話,他本人是會諒解這一點的。他在一次抑制不住巨大喜悅時寫道:“我沉湎在神聖的狂喜之中……我的書已經完稿。它不是會被我的同時代人讀到就會被我的子孫後代讀到──這是無所謂的事。它也許需要足足等上一百年才會有一個讀者,正如上帝等了6000年才有一個人理解他的作品。”
但是經過幾十年的歷程,克卜勒定律的意義在科學界逐漸明朗起來。實際上在17世紀晚期,有一個支持牛頓學說的主要論點認為克卜勒定律可以從牛頓學說中推導出來,反過來說只要有牛頓運動定律,也能從克卜勒定律中精確地推導出牛頓引力定律。但是這需要更先進的數學技術,而在克卜勒時代則沒有這樣的技術、就是在技術落後的情況下,克卜勒也能以其敏銳的洞察力判斷出行星運動受來自太陽的引力的控制。
主要著作
 Mysterium cosmographicum
Mysterium cosmographicum 《宇宙的奧秘》(Mysterium cosmographicum)(1596)
《天文學的光學需知》(Astronomiae Pars Optica)(1604)
《蛇夫座腳部的新星》(De Stella Nova in Pede Serpentarii)(1606)
《新天文學》(Astronomia nova)(1609)
《折光學》(Dioptrice)(1611)
《世界的和諧》(Harmonices Mundi)(1618)
《哥白尼天文學概要》(Epitome astronomiae Copernicanae)(1618-1621)
《魯道夫星表》(Tabulae Rudolphinae)(1627)
人物影響
【美國發射“克卜勒”號太空望遠鏡】
美國東部時間2009年3月6日,世界首個用於探測太陽系外類地行星的“克卜勒”號太空望遠鏡在美國卡納維拉爾角空軍基地等待發射升空。當日22時50分,搭載太空望遠鏡的火箭成功升空。
 1971年德國發行的克卜勒紀念郵票。
1971年德國發行的克卜勒紀念郵票。 美國東部時間2009年3月6日22時50分,世界首個用於探測太陽系外類地行星的“克卜勒”號太空望遠鏡在美國卡納維拉爾角空軍基地發射升空。從美國航天局網站獲得的這幅圖像描述的是銀河系以及“克卜勒”號太空望遠鏡搜尋太陽系外類地行星的範圍。新華社發
美航天局發射“克卜勒”太空望遠鏡
美國東部時間2009年3月6日22時50分(台北時間7日11時50分),世界首個用於探測太陽系外類地行星的飛行器——“克卜勒”太空望遠鏡在美國卡納維拉爾角空軍基地發射升空。
“克卜勒”將升空 三年內或將發現外星“地球”
美國航空航天局(NASA)的克卜勒衛星,預計於台北時間3月7日中午11:48分發射升空,將為地外生命的搜尋翻開新的一頁。這項以十六、十七世紀德國天文學家約翰內斯·克卜勒(Johannes Kepler)的名字來命名的探測計畫,將用三年多的時間來研究一批恆星,尋找恆星亮度上微弱的周期性變暗——這是恆星周圍有行星圍繞的跡象。


