定律定義
克卜勒在《宇宙和諧論》發表的表述：每一個行星都沿各自的橢圓軌道環繞太陽，而太陽則處在橢圓的一個焦點中。
克卜勒第一定律數學推導
設定
克卜勒第一定律這樣，角速度是
克卜勒第一定律對時間微分和對角度微分有如下關係：
克卜勒第一定律根據上述關係，徑向距離 對時間的導數為：
克卜勒第一定律再求一次導數：
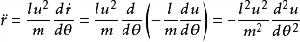克卜勒第一定律
克卜勒第一定律代入徑向運動方程
，
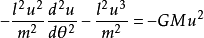克卜勒第一定律
克卜勒第一定律將此方程除以
，則可得到一個簡單的常係數非齊次線性全微分方程來描述行星軌道：
克卜勒第一定律為了解這個微分方程，先列出一個特解
克卜勒第一定律再求解剩餘的常係數齊次線性全微分方程，
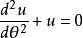克卜勒第一定律它的解為
克卜勒第一定律
克卜勒第一定律這裡，
與
是常數。合併特解和與齊次方程解，可以得到通解
克卜勒第一定律
克卜勒第一定律選擇坐標軸，讓
。代回
，
克卜勒第一定律
克卜勒第一定律其中，
是離心率。
克卜勒第一定律這是圓錐曲線的極坐標方程，坐標系的原點是圓錐曲線的焦點之一。假若
，則
所描述的是橢圓軌道。這證明了克卜勒第一定律。
發展簡史
克卜勒1596年出版《宇宙的神秘》一書受到 第谷的賞識，應邀到布拉格附近的天文台做研究工作。1600年，到布拉格成為第谷的助手。次年第谷去世，克卜勒成為第谷事業的繼承人。
第谷去世後克卜勒用很長時間對第谷遺留下來的觀測資料進行分析，他在分析火星的公轉時發現，無論按哥白尼的方法還是按托勒密或第谷的方法，算出的軌道都不能同第谷的觀測資料相吻合，他堅信觀測的結果，於是他想到火星可能不是作當時人們認為的勻速圓周運動，他改用各種不同的幾何曲線來表示火星的運動軌跡，終於發現了“火星沿橢圓軌道繞太陽運行。
克卜勒在1619年出版的《 宇宙和諧論》發表該定律。
定律影響
克卜勒第一定律克卜勒第二定律：在相等時間內，太陽和運動中的行星的連線（向量半徑）所掃過的面積都是相等的。 這一定律實際揭示了行星繞太陽公轉的角動量守恆。
克卜勒第三定律：是指繞以太陽為焦點的橢圓軌道運行的所有行星，其橢圓軌道半長軸的立方與周期的平方之比是一個常量。這裡，a是行星公轉軌道半長軸，T是行星公轉周期，K是常數，其大小隻與中心天體的質量有關。
