定義
各邊相等,各角也相等的多邊形叫做正多邊形 !
 正多邊形
正多邊形尺規作圖
直尺、圓規和量角器可以畫出任意正多邊形。 但是在古希臘時,作圖只使用沒有刻度的直尺(unmarked ruler)和圓規(compass)。 用尺規作正偶邊形如2n,3×2n,5×2n等正多邊形並非難事。 用尺規作正偶邊形如2n,3×2n,5×2n等正多邊形並非難事。 但對正奇邊形如3,5,7,9,11,13,15等的作圖,在當時是件困難的事,而且並非全都可以作圖成功。 1798年,德國數學家高斯只有19歲,他成功的以圓規直尺做出一個正十七邊形,並證明了正奇邊形的邊數只有是費馬質數或不同的費馬質數乘積才可以尺規作圖出來,當高斯去世後,人們為了紀念這位偉大的數學家,在他的故鄉(Brunschweig)的紀念碑上刻了這個正17邊形。
■費馬質數相關
費馬質數是質數且型如,k是非負正整數.
k:0 1 2 3 4 5
3 5 17 257 65537 4294967297
當k=0,1,2,3,4,5時,都是質數,但一般猜測k>5時,都不是費馬質數。 由於我們目前知道只有五個費馬質數存在,所以用圓規可以做出的正奇邊形是3,5 , 1 7,257,65537,以及這五個數的兩兩相乘積。 如3×5,3×17,17×257等共31個。 如3×5,3×17,17×257等共31個。 而最大的正奇邊形的邊數是 4294967297。 邊數小於100,可以尺規作圖的正多邊形如下:
3 4 5 6 8 10 12 15 16 17 20 24
30 32 34 40 48 51 60 64 68 80 85 96
鑲嵌的規律
在正多邊形中,只有三種能用來鋪滿一個平面而中間沒有空隙,這就是正三角形、正方形、正六邊形。因為正三角形的每一個角等於60度,六個正三角形拼在一起時,在公共頂點上的六個角之和等於360度;正方形的每個角等於90度,所以四個正方形拼在一起時,在公共頂點上四個角的和也剛好等於360度;正六邊形的每個角等於120度,三個正六邊形拼在一起時,在公共頂點上的三個角之和也等於360度,如果用別的正多邊形,就不能達到這個要求。例如正五邊形的每隻角等於108度,把三個正五邊形拼在一起,在公共頂點上三個角之和是108度*3=324度,小於360度有空隙。而空隙處又放不下第四個正五邊形,因為108度*4=432度,大於360度。
內角的計算
計算內角的公式為:(邊數-2)*180度
有關概念
正多邊形的外接圓
把圓分為n(n≥3)等份,依次連線各分點所得的多邊形就是這個圓的內接正n邊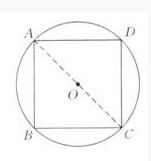 1
1形,也就是正n邊形的外接圓。