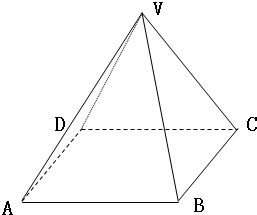
體積公式
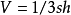 四稜錐
四稜錐定義與判定
四稜錐是由四個三角形和一個四邊形構成的空間封閉圖形,而正四稜錐,則是底面為正方形,四個三角形為全等三角形而且是等腰三角形。
 四稜錐
四稜錐【生活中範例】:金字塔就是正四稜錐
體積公式推導
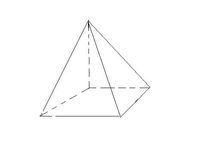
在四稜錐上做一個與四稜錐B1-ABCD同底等高的四稜柱A1B1C1D1-ABCD出來,沿底面的對角線BD與稜錐的頂角B1所在的面把四稜錐切開,把四稜錐的問題轉化成三稜錐的問題。
 四稜錐
四稜錐這時候,兩個三稜柱與兩個三稜錐都分別是等底等高。他們的體積是分別相
等的。若能證明三稜錐體積是1/3sh,即可證明四稜錐的體積計算公式1/3sh。
連線A D1之後,發現三稜柱是由三個三稜錐組成,只要證明這三個三稜錐B1-ABD,A-A1B1D1,A-D1B1D體積相等就可以了。
B1-ABD與A-A1B1D1等底等高,所以體積相等。
B1-ABD換個角度看其實就是A-B1BD,A-B1BD與A-D1B1D等底等高,所以體積相等。所以B1-ABD與A-D1B1D體積相等。
也就是說組成三稜柱的這三個三稜錐體積相等,所以三稜錐體積是1/3sh
所以四稜錐的體積計算公式1/3sh。
四稜錐的底面面積S加頂點A'面積0除以2的平均面積1/2S的一個四稜柱乘以高h,就是四稜錐體積:
V=1/3(S+0)h=1/3Sh