定義
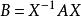矩陣相似設A，B為數域P上兩個n階矩陣，如果可以找到數域P上的n階可逆矩陣X，使得 ，則稱A相似於B，記作A~B。
性質
(1) 若A相似於B，則A等價於B（即A可通過初等變換化為B）
(2) 若A相似於B，則tr(A)=tr(B)
(3) 若A相似於B，則|A|=|B|
以上三條反之皆不成立
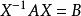矩陣相似證明:若A~B，則存在可逆矩陣X使得
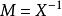矩陣相似
矩陣相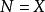似
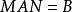矩陣相似令 ， 則 ，即A與B等價，(1)成立
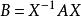矩陣相似因 ，於是有
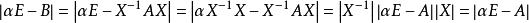矩陣相似即A與B有相同特徵值多項式，因而有相同的特徵值，故(2)(3)也成立。
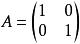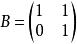矩陣相似
矩陣相似反例： ，
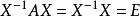矩陣相似顯然A與B等價，並且tr(A)=tr(B)，|A|=|B|，但A與B不可能相似(因A=E，對任意的n階可逆矩陣X，都有 )。
相似是矩陣間的一種重要關係，這種關係具有以下三個性質：
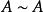矩陣相似
矩陣相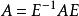似
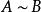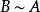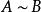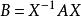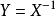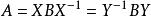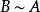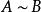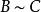矩陣相似
矩陣相似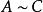
矩陣相似 矩陣相似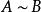 矩陣相似
矩陣相似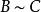
矩陣相似 矩陣相似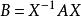 矩陣相似
矩陣相似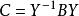
矩陣相似 矩陣相似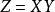 矩陣相似 矩陣相似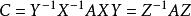
矩陣相似
矩陣相似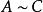
矩陣相似 矩陣相似1.反身性： 。這是因為 （其中 為單位矩陣，下同）。2.對稱性：如果 ，那么 。事實上如果 ，那么有X使 ，令 ，就有 ，所以 。3.傳遞性：如果 ， ，那么 。因為若，，即存在X，Y使 ， 。令 ，就有 ，因此有 。(具有以上三個性質的關係統稱為等價關係)
矩陣相似充分必要條件
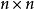矩陣相似設A，B是數域P上兩個 矩陣：
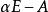矩陣相似
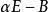矩陣相似(1) A與B相似的充分必要條件是它們的特徵矩陣 與 等價。
(2) A與B相似的充分必要條件是它們有相同的不變因子。
(3) 兩個同級複數矩陣相似的充分必要條件是它們有相同的初等因子。
套用
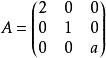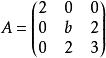矩陣相似
矩陣相似例：已知A~B，其中 ， 。
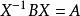矩陣相似
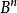矩陣相似(1)求a,b的值；(2)求可逆矩陣X使 ；(3)求 。
解：(1)因tr(A)=tr(B)及|A|=|B|可得a=5,b=3
(2)顯然A的特徵值為2，1，5，即B的特徵值也為2，1，5
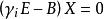矩陣相似
矩陣相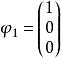似
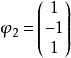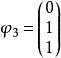矩陣相似
矩陣相似由 可得對應特徵向量 ， ，
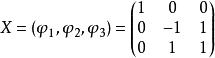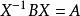矩陣相似 矩陣相似令 ，則有 。
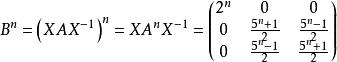矩陣相似(3) 。
