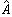密度矩陣
正文
又稱統計算符,描述統計系綜中力學體系的量子運動狀態的分布的矩陣。用求跡符號tr表示取後面矩陣所有對角元之和,則任意力學量
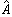 的統計平均值
的統計平均值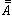 可用該力學量的矩陣
可用該力學量的矩陣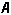 與統計系綜的密度矩陣
與統計系綜的密度矩陣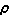 表達為
表達為 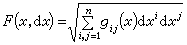
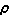 )=1,
)=1,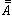 =tr(
=tr(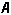
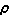 )。
)。 若q為力學體系所有自由度的坐標的簡寫,k為該體系量子運動狀態的完全描述的簡寫。引入正交歸一化並且完備的基本函式系{ψk(q)},並將系綜中每個量子力學體系的薛丁格波函式對基本函式系展開,如
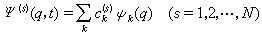 。
。
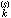 為時間t的函式,滿足與(s)無關的同樣的按幾率歸一化的條件(*表示取複數共軛)。
為時間t的函式,滿足與(s)無關的同樣的按幾率歸一化的條件(*表示取複數共軛)。 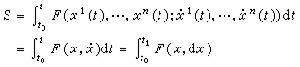
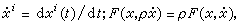 ,
,
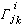 ,而 ρkk為系綜中力學體系處在運動狀態 k上的幾率。任意力學量┮對力學體系(s)的量子平均值為
,而 ρkk為系綜中力學體系處在運動狀態 k上的幾率。任意力學量┮對力學體系(s)的量子平均值為 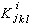 ,
,
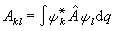 構成該力學量的矩陣。所以該力學量對系綜的統計平均值為
構成該力學量的矩陣。所以該力學量對系綜的統計平均值為 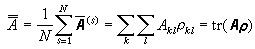 ,
,
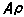 代表矩陣乘積。如不按幾率歸一化,密度矩陣比上面定義者可差常數因子。
代表矩陣乘積。如不按幾率歸一化,密度矩陣比上面定義者可差常數因子。 隨時間的變化 將薛丁格波函式的展開式代入薛丁格方程
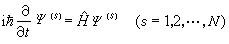 ,
,
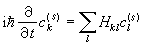 (s=1,2,…,N,k=所有值),
(s=1,2,…,N,k=所有值),
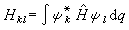 為哈密頓量彑的矩陣元;因為哈密頓量為厄密算符,有
為哈密頓量彑的矩陣元;因為哈密頓量為厄密算符,有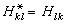 。利用展開係數隨時間變化的上述方程及其複數共軛,可以推出
。利用展開係數隨時間變化的上述方程及其複數共軛,可以推出 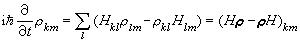
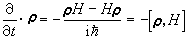 ,
,
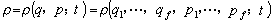
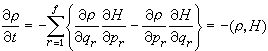 ,
,
單電子密度矩陣 當量子力學體系為n電子體系,如採用哈特里-福克近似而引入單電子波函式時,常如下定義單電子密度矩陣,亦簡稱為密度矩陣:
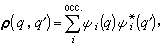
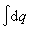 時對三維空間坐標積分並對自旋坐標求和,上述單電子密度矩陣是歸一為總電子數
時對三維空間坐標積分並對自旋坐標求和,上述單電子密度矩陣是歸一為總電子數 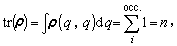
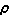 (q,q),而在q和q'處出現任一對電子的幾率為行列式
(q,q),而在q和q'處出現任一對電子的幾率為行列式 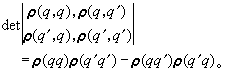
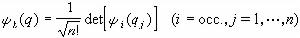
參考書目
P.A.M.狄拉克著,陳鹹享譯:《量子力學原理》,科學出版社,北京,1979。(P.A.M.Dirac,The Principles of Quantum Mechanics,4th ed.,Clarendo Press,Oxford,1958.)
P. A. M.Dirac,Proc.Camb.Phil.Soc.,Vol.25, p.62,1929; Vol.26, p.376, 1930; Vol.27, p.240, 1931.