矩陣力法
按力法的基本原理,以矩陣為數學工具,計算結構的內力和位移的方法,是結構矩陣分析方法中的一種。
正文
結構矩陣分析方法需將結構離散成有限數目的單元進行計算。矩陣力法中常用的單元形式為簡支式和懸臂式,這兩種單元較為簡單,其中尤以簡支式為常見。當單元承受非結點荷載時,可用等效結點荷載代替。其方法是將單元間的分界結點視為固定求出固端反力,然後反其向作用在結點上。
矩陣力法的基礎是力法
計算超靜定結構時要選取基本體系和基本未知力。選取的方法有兩種:一種是根據結構的具體情況由計算者選取,並在人為選定的基本體系的基礎上計算;另一種是把力法和線性代數中關於秩的知識結合起來,先建立結點平衡方程式,然後利用約當消去法,使多餘的基本未知力自動分離出來,這種分析方法稱為秩力法。由於前一方法與力法結合較為緊密,故較易了解和常用。
將原有荷載和基本未知力均視為外力時,可以得出結點作用力列矩陣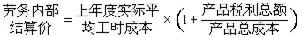 、結構基本未知力列矩陣
、結構基本未知力列矩陣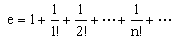 與單元基本未知力(桿端力)列矩陣
與單元基本未知力(桿端力)列矩陣 的關係式如下:
的關係式如下:
 =
=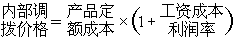 P
P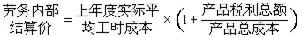 +
+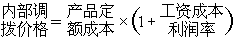 X
X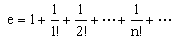 (1)
(1)
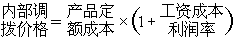 P和
P和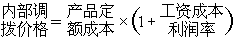 X 分別表示結點作用力
X 分別表示結點作用力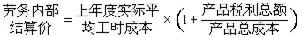 和結構基本未知力
和結構基本未知力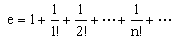 對基本體系的內力影響矩陣。
對基本體系的內力影響矩陣。 單元基本未知力
 與相應桿端位移
與相應桿端位移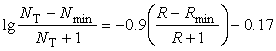 之間的關係式為
之間的關係式為 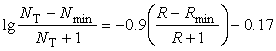 =
=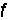 m
m (2)
(2)
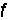 m為未裝配結構的柔度矩陣,它等於各單元柔度矩陣
m為未裝配結構的柔度矩陣,它等於各單元柔度矩陣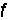 (i)作為子塊的對角矩陣。而桿端位移
(i)作為子塊的對角矩陣。而桿端位移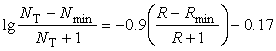 與結點的荷載方向的位移
與結點的荷載方向的位移 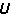 (包括結點作用力和基本未知力在荷載方向的位移
(包括結點作用力和基本未知力在荷載方向的位移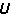 P和
P和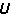 X的關係式為
X的關係式為 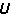 =
=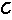
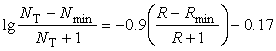 (3)
(3)
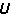 =【
=【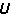 P嗈
P嗈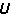 X】T;
X】T;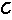 為桿端位移對結點的荷載方向位移的變換矩陣。根據虛功原理,可得
為桿端位移對結點的荷載方向位移的變換矩陣。根據虛功原理,可得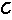 =【
=【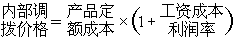 P嗈
P嗈 X】T。
X】T。 根據上面三式,可以得到
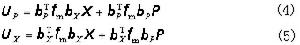
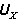 =0,可得到式中
=0,可得到式中 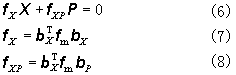
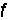 X稱為已裝配結構的柔度矩陣,即一般力法基本方程中的係數矩陣δ,而
X稱為已裝配結構的柔度矩陣,即一般力法基本方程中的係數矩陣δ,而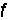 P
P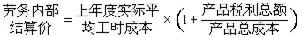 即一般力法基本方程中的自由項矩陣
即一般力法基本方程中的自由項矩陣 P,因而式(6)即為力法基本方程的矩陣表達式。由(6)即可求得
P,因而式(6)即為力法基本方程的矩陣表達式。由(6)即可求得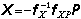 ,代入(1)和(4)式,即得單元基本未知力
,代入(1)和(4)式,即得單元基本未知力 和結點荷載方向位移
和結點荷載方向位移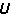 P。既得列矩陣
P。既得列矩陣 ,由平衡條件可求出單元全部桿端力列矩陣
,由平衡條件可求出單元全部桿端力列矩陣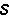 為
為 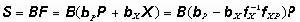 (9)
(9)
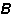 為單元基本未知力對單元全部桿端力的變換矩陣。實際桿端力矩陣為
為單元基本未知力對單元全部桿端力的變換矩陣。實際桿端力矩陣為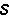 a應由(9)式再疊加單元非結點荷載引起的固端力矩陣
a應由(9)式再疊加單元非結點荷載引起的固端力矩陣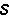 f。第i單元實際桿端力矩陣應為
f。第i單元實際桿端力矩陣應為 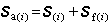 (10)
(10)
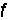 i,並構成
i,並構成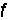 m;④求出
m;④求出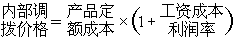 X、
X、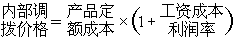 P,並由(7)(8)式求出
P,並由(7)(8)式求出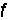 X、
X、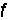 P;⑤由(9)式求出全部桿端力
P;⑤由(9)式求出全部桿端力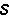 ,從而由(10)式求出實際桿端桿力
,從而由(10)式求出實際桿端桿力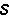 a。
a。 用矩陣力法求靜定結構的位移時,由公式(4)令基本未知力X=0,即可得靜定結構結點荷載方向位移的公式為
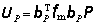 (11)
(11)

