特點
矩陣數學表達力強
 矩陣位移法
矩陣位移法矩陣數學表達力強,運算簡潔方便並且適於計算機組織運算,是用計算機進行結構數值分析的最強有力的數學工具。
矩陣位移法與結構力學的力法和位移法相對應,也就是結構的矩陣分析方法。
矩陣位移法方便編製程序
矩陣位移法便於編製程序,因而在工程界得到廣泛套用。
矩陣位移法並不因採用矩陣數學的描述手段,而改變位移法的基本原理。它與位移法的區別僅僅在於表達形式不同。
矩陣位移法的基本原理
按位移法的基本原理運用矩陣計算內力和位移的方法。是結構矩陣分析方法中的一種,其基本未知數是結點位移,由於矩陣位移法較矩陣力法更適宜編制通用的計算程式,因而得到了更為廣泛的套用。
結構矩陣分析方法首先把結構離散成有限數目的單元,然後再合成為原結構,因而也屬於有限元法。矩陣位移法常用的單元形式為一直桿。對於曲桿,如拱結構,雖然也可取曲桿作為單元,但單元分析較煩,為簡化起見,可將它化成折線來處理,每一直線段作為一單元。當單元承受非結點荷載時,可
用等效結點荷載代替。其方法是將單元間的分界結點作為固端求出固端反力,然後反其向作用在結點上。
根據結構變形後要滿足幾何方面的相容條件(變形條件),結點位移矩u與桿端位移矩之間存在關係式
(1)式a表示u的變換矩陣。
桿端位移矩與桿端力矩s之間的關係式為 s=k
(2)
式km稱為未裝配結構的剛度矩陣,它等於各單元剛度矩k(i) 作為子塊的對角矩陣。 其元素可直接按結點單位位移引起的反力而求得。由於單元坐標並不一定是整體結構坐標,因而求得的單元剛度矩k(i) 需通過坐標變換轉化為整體坐標下的單元剛度矩陣。
根據結點作用力與匯交於該結點的桿端力保持平衡關係,可以得到桿端s與結點作用的關係式為=ds(3)式d為桿端力矩s 對結點作用力矩的變換矩陣。
根據虛功原理,可daT。
根據上面三式,可以得到=K(4)
KaTm (5)
式(5)K稱為已裝配結構的剛度矩陣或整體剛度矩陣。
通過式(5)獲得總剛度矩陣K的方法稱為剛度法。因為位移變換矩a的階數相當高,運算中須占大量的存貯單元,因而在組合整體剛度矩陣時,常採用直接把單元剛度矩陣的元素輸送到K中的直接剛度法,該方法是將各單元中相同腳標的元素直接相加而組成整體剛度矩陣。在單元剛度矩陣中,對於近端結點剛度矩陣係數kjj,由於匯集於該結點j的所有單元都可作出貢獻,因而在整體剛度矩陣中可有若干項相加,為匯集於j結點的所有單元。由於它不必通過式(5)進行計算,運算方便,因此其套用比剛度法更為廣泛。
由於支座約束方向的結點位移通常為零或為已知值,因而可將全部結點位u分為兩部分,一部分是不受支座約束的位ur,另一為沿支座約束方向的結點位uR。由此(4)式變成展開上式得 (7)(8)
uR=0時(7)式變成: r=Kur (7′)
式中Kr為已裝配結構相應不受支座約束的位移的剛度矩陣,實際上即為一般位移法基本方程中的係數矩陣K,該矩陣亦可直接按柔度矩陣求逆而得到。r即為一般位移法基本方程的自由項矩r(一般位移法中,Kr在方程同一邊,因rR差一符號)。因而(7′)式即為位移法基本方程的矩陣表達式。
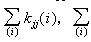 公式
公式根據(7)或(7′)式即可求ur。再由(1)、(2)式即可求得桿端s,實際桿端sa應再疊加單元上非結點荷載引起的固端sf。第i單元的實際桿端力應為 sa(i)k(i(i)sf(i)
(9)
矩陣位移法計算桿端力的步驟
矩陣位移法計算桿端力的步驟為:
①劃分單元,求出等效結點荷載;
②求單元剛度矩k(i),並轉換為整體坐標的單元剛度矩陣;
③由(5)式或直接剛度法求出整體剛度矩陣K;
④求出Krr;
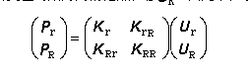 公式
公式⑤由(7′)式求出結點位ur,再由(1)、(2)式求出桿端s,實際桿端力應再疊sf, 即由(9)式確定。

