桿繫結構的靜力分析
正文
桿繫結構是用桿件相互聯結而組成的幾何不變體系,如多跨靜定梁、連續梁、桁架、剛架、拱、懸索結構、網架結構和曲梁等均為桿繫結構。桿繫結構的靜力分析是指在已知靜力荷載下桿繫結構的內力和位移計算。桿繫結構分為靜定結構和超靜定結構。凡是僅用靜力平衡原理即可求出結構的全部內力和反力時,稱結構為靜定結構;否則為超靜定結構。超靜定結構可用力法、位移法或混合法等求解。在求得內力後,靜定結構和超靜定結構均可用位移計算公式或其他方法求得結構中任意指定點的位移。較複雜的超靜定結構,由於其計算工作量很大,在20世紀30~50年代期間,曾發展了許多近似法、漸近法及實用的簡化方法。這些方法在當時曾解決過許多工程結構的計算問題,也推動了結構力學的發展。但隨著電子計算機的發展和普及,適合於計算機的矩陣力法、矩陣位移法及有限元法等已成為分析複雜問題的主要方法。
桿繫結構還可分為平面結構和空間結構。當結構的全部桿件、支座及作用力均位於同一平面時,稱結構為平面結構;否則即為空間結構。工程中的絕大多數結構都是空間結構。但在許多情況下往往可以引入一些適當的假定,把它們簡化為平面結構,從而避免複雜的計算並取得精度符合工程要求的結果。在計算機發展後,習慣上常簡化為平面結構的桁架和剛架(見框架)等,已逐步轉向按空間結構計算。
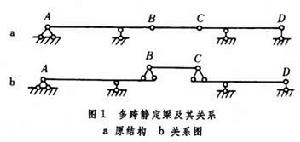
多跨靜定梁 通常的多跨靜定梁由多個單跨靜定梁相互支承或聯結而成。各單跨靜定梁可按其相互間的支承關係分為基本部分(圖1a中的AB及CD)和附屬部分(圖1a中的BC)。表現這種相互關係的圖1b,稱為關係圖。計算多跨靜定梁的反力及內力時,都可根據靜力平衡原理決定。計算時,按先附屬部分後基本部分的順序,逐層取隔離體來進行。
 桿繫結構的靜力分析
桿繫結構的靜力分析桁架 由若干只產生軸力的桿件用鉸鏈聯結成的幾何不變的結構稱為桁架。為使桁架桿件只產生軸力,桁架的計算常作以下假定:①桁架中每根桿件的兩端由理想鉸聯結;②每根桿件的軸線必須是直線;③所有桿件的軸線都只交於所聯理想鉸的幾何中心。④荷載均只作用於理想鉸的幾何中心。在此條件下所算得的各種應力稱為主應力。實際上各種桁架結構不可能完全滿足上述各假定,因而桿件將產生彎曲,由這種彎曲而在桿件中所引起的軸向應力稱為次應力。鋼桁架如設計得較合理,次應力一般不太大;鋼筋混凝土或預應力混凝土桁架,由於其結點剛度大、桿件粗短,次應力的影響不能忽視。
靜定平面桁架可先求出反力,然後用結點法或截面法求桿件內力。其中又分數解法和圖解法。結點法每次截取一個結點為隔離體,可建立兩個投影方程;只要適當選定求解次序,使每次求解時未知力不超過兩個,即可求出全部桿件內力。截面法截取桁架的一部分為隔離體,可根據靜力平衡方程求解;此法特別適合於求指定桿件內力。超靜定桁架和空間桁架可通過矩陣法用計算機求解。
剛架 由若干桿件借剛結點聯結成的結構稱為剛架(圖2a),多用鋼筋混凝土或鋼材建造,剛架結構多為空間剛架,但許多空間剛架可分解為平面剛架進行計算。剛架可分為靜定剛架和超靜定剛架,但工程中所套用的主要是超靜定剛架。
 桿繫結構的靜力分析
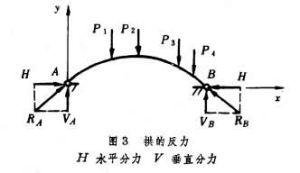
桿繫結構的靜力分析拱 主要受軸向壓力作用,故常用抗壓強而抗拉弱的材料建造。單跨拱可按所設定的鉸的多少分為三鉸拱、雙鉸拱及無鉸拱等,單鉸拱套用不多。三鉸拱是靜定結構,余者為超靜定結構。拱在豎向荷載作用的反力R如圖3。
 桿繫結構的靜力分析
桿繫結構的靜力分析超靜定拱常用力法計算,但因軸線為曲線且截面常沿軸線變化,因此在計算前先將拱軸分成若干段,並將各段視為等截面直桿,然後用總和法計算。在使用計算機時,可用矩陣力法或矩陣位移法,但也要將拱分段處理,否則需要用曲桿單元。此外,當拱的曲率較大時,還要注意應計及曲率的影響。
懸索結構 用只能承受拉力的懸索構件與其他承重構件組成的結構稱為懸索結構,如通常用高強度鋼材做懸索,它能承受很大的拉力而自重較小,因此懸索結構主要用於各種大跨度結構,如懸索橋、斜張橋、懸索屋蓋等。懸索是只能受拉力的柔性構件,且強度高、斷面小,因此懸索結構的整體剛度較小,在荷載作用下變形較大。
跨度較小或結構整體的剛度較大時,懸索結構可用通常的小變形理論,即線性理論求解。此時,懸索結構與普通的組合結構相當,一般可採用矩陣位移法或有限元法計算。但在跨度較大,懸索內拉力很大時,即使懸索本身仍處於線性變形階段,也要考慮變形的影響。此時應採用撓度理論,即二階理論進行計算。
對於雙向正交網索結構還可以將索網視為薄膜,建立其平衡微分方程和變形協調方程,並假定一垂直變位曲面的形式,令由此導出的假想荷載與實際荷載儘量接近,即可求得滿足邊界條件的近似解。
交叉梁系和網架結構 布置在同一平面的兩組或多組梁在交叉處相互聯結而構成一個整體的結構稱為交叉梁系;兩組或多組桁架聯結成的結構稱為網架。交叉梁系常用做樓面系、橋面系或船舶甲板之骨架;網架結構主要用做大跨度屋蓋。
這兩種結構都是空間結構,且各組梁或桁架組成一個整體,共同作用,不宜分解為平面結構計算,因此常採用矩陣位移法按空間結構求解。對於交叉梁系,由於荷載為垂直於結構平面的豎向荷載,常可忽略桿件軸向變形及結點繞豎直軸z的轉角的影響,因此每個結點可只考慮3個自由度,即繞x、r軸的轉角及撓度。對於網架結構,常用的一種近似解法是將組成網架的每一片桁架用一根相當的梁代替,從而將網架簡化為一相應的交叉梁系。然後按交叉梁系計算,並以梁系的內力推算桁架上、下弦桿及腹桿內力。這種近似解法有時也能滿足工程設計的要求。
曲梁 梁的軸線為曲線時稱為曲梁。軸線及荷載均位於同一平面時稱為平面曲梁,否則為空間曲梁。空間曲梁的力學特徵與直梁有很大區別,如在荷載作用下空間曲梁通常產生彎曲和扭轉變形,且兩種變形相互耦聯。扭轉變形所引起的撓曲變形較大,一般不能忽略。
Β.З.符拉索夫為曲梁分析建立了基本微分方程。這些方程描述了曲梁單元體的荷載與變形的關係。分析時,可將作用於該單元體上的荷載分解為:沿單元體的3根相互正交的軸線作用的3個分布力和3個分布扭矩。由此建立的微分方程可用閉形法和傅立葉級數法求解,也可用差分法等其他近似解法。
若結構由幾根曲梁和橫樑組成,則可按交叉梁系處理。
參考書目
金寶楨主編:《結構力學》,人民教育出版社,北京,1964。
土木學會編,王道堂等譯:《日本土木工程手冊·結構力學》,中國鐵道出版社,北京,1982。(土木學會編:土木工學)ハンドブック,技報堂,東京,1974。)

