位移法

位移法，是超靜定結構分析（見桿繫結構的靜力分析）的基本方法之一，也稱變位法或剛度法，通常以結點位移作為基本未知數。位移法有兩種計算方式，一種是套用基本結構列出典型方程進行計算，另一種是直接套用轉角位移方程建立原結構上某結點或截面的靜力平衡方程進行計算，後者常稱為轉角位移法。

正文

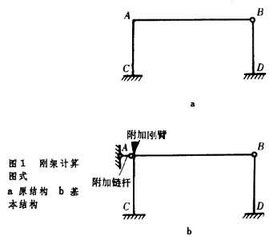
基本結構　用位移法計算超靜定結構時，須先確定基本未知數,即獨立的結點角位移和線位移的總數n（如圖1a，n＝2。但忽略其軸向變形）。然後在這些結點上相應地加上阻止轉動的附加剛臂或阻止移動的附加鏈桿，使結構變成一系列離散部分的集合。這樣形成位移法的基本結構（如圖1b）。通常各離散部分均為等截面超靜定梁。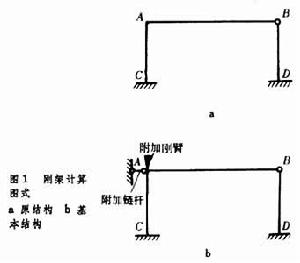

位移法

典型方程　為使基本結構的變形和內力情況與原結構相同，必須使基本結構承受與原結構相同的荷載（包括溫度變化、支座沉陷等因素），並使附加約束髮生與原結構相同的位移。因為原結構上本無附加約束，所以基本結構上所有附加約束中的約束反力都應等於零。據此建立位移法典型方程：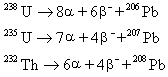

式中係數Knk表示在基本結構中第i個附加約束由於第k個附加約束髮生單位位移所引起的反力矩或反力，係數矩陣是對稱的；自由項RiP 表示在結構上第i個附加約束由於荷載作用所引起的反力矩或反力；基本未知數xi是第i個結點的角位移或線位移，i＝1，2，…，n。
為了求得典型方程中的係數和自由項，須分別繪製基本結構在各附加約束髮生單位位移時的 Mi圖及在荷載作用下的MP圖,並利用結點或截面的平衡條件求出各係數和自由項。由於基本結構中各桿通常都是單跨超靜定梁，它們在荷載及支座發生各種單位位移情況下的固端彎矩公式都可以先行用力法或其他方法導出，這樣的公式稱為轉角位移方程。如等截面兩端固定梁當發生圖2所示的位移時，其轉角位移方程為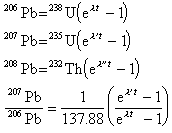

式中i＝EI/l；ψ＝墹/l；E為材料彈性模量；I為截面慣性矩;MF為荷載引起的固端彎矩。對變截面桿也可以導出其轉角位移方程並繪製相應的圖表備用。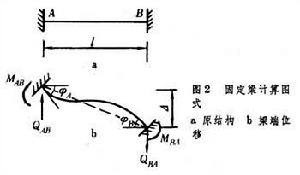

位移法

轉角位移法　轉角位移法不必對基本結構分別作各Mi和MP圖,也不單獨計算各係數和自由項，而是直接套用轉角位移方程，將各桿端彎矩或剪力表示為未知結點位移的函式。然後依次截取各含有待求角位移的結點為隔離體，根據所有匯交於這一結點的各桿近端作用於該結點的彎矩及結點力矩荷載的代數和應等於零，而建立結點平衡方程；再依次作截面，截取各含有待求線位移結點的隔離體，在該線位移方向上列出力的投影的平衡方程，即得截面平衡方程，這樣建立起來的平衡方程與典型方程完全相同。
解算典型方程求得各基本未知數xi後，即可按疊加原理或轉角位移方程求得結構內力。

配圖

相關連線