力法
正文
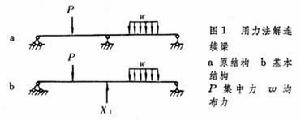
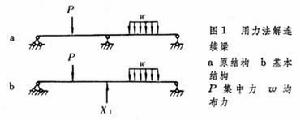
以與多餘聯繫相應的多餘未知力作為基本未知數的分析超靜定結構（見桿繫結構的靜力分析）的基本方法之一。基本結構 為了暴露這些多餘未知力，必須將多餘聯繫截斷或撤除，再用相應的內力或反力代替它們的約束作用，如圖1a所示的連續梁，撤除中間支座後，可用未知反力X1代替原有的支座約束，這樣就將原結構轉變為幾何不變的靜定結構，稱為力法的基本結構。若能設法確定多餘未知力，則整個計算就可按靜定結構處理。
力法根據疊加原理，基本結構上任意一點的總位移等於多餘未知力和原荷載分別作用時所產生位移的總和，即
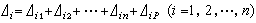；若用δ 表示單位力所引起的位移，則有墹i1＝X1δi1，墹i2＝X2δi2,…，墹in＝Xnδin等。由於原結構上各多餘聯繫本來是連續不斷的，為了使基本結構與原結構的變形一致,應該有墹i＝X1δi1+X2δi2+…+Xnδin+墹iP =0(i=1,2,…，n)這組方程稱為力法的典型方程。它也可由最小虛力原理推出。位於主對角線上的主係數恆為正值。位於主對角線兩側對稱位置上的副係數，可能為正、為負或為零。由位移互等定理，有δkj＝δji,這樣可減輕一半的計算工作。由荷載引起的位移墹iP(稱自由項)，也可能為正、為負或為零。由典型方程解出多餘未知力，即可用疊加原理計算原結構的內力。如原結構的彎矩M為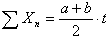 
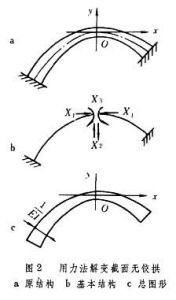
對於變載面無鉸拱三次超靜定結構（圖2a），可採用彈性中心法。消去典型方程中的全部副係數，首先在其軸線頂點O截開,用成對的軸力X1、剪力X2和彎矩X3作為多餘未知力(圖2b)，再以O點作為坐標原點,X1和X2作用線作為x、y坐標軸，則在單位多餘力作用下的彎矩為
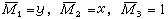
力法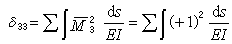
。式中ds為沿拱軸的微段長；E為材料的彈性模量；I為桿件的截面慣性矩。若將1/EI看作是微段的寬度,則ds/EI可看作是沿拱軸變化的彈性微面積或彈性重量，因而δ33可看成沿拱軸描畫的由彈性微面積組成的總圖形（圖2c）。副係數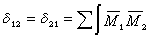 
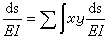，則可看成總圖形對x軸和y軸的慣性積；而δ13=δ31以及δ23=δ32，則可分別看成總圖形對x 軸和y軸的靜矩。 如果把坐標原點移取在總圖的重心上，稱做彈性中心，且使x、y軸平行於總圖形的主軸，則其靜矩和慣性積都將成為零，因而全部副係數均將消失。這樣，力法典型方程變換為三個獨立的方程，使計算工作大為簡化，稱彈性中心法。為了不改變原結構的受力和變形狀態，一般用剛臂把截口聯結到彈性中心，並在彈性中心上分解三對多餘未知力X1、X2、X3進行計算。
參考書目
李廉錕主編：《結構力學》（第二版），高等教育出版社，北京，1984。
