發現者
姓名:喬治·尼古拉斯·亞歷山大·皮克(1859~1943)
全名:George Alexander Pick
國籍:奧地利
定理定義
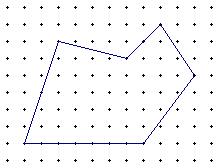 a=39,b=14,s=45
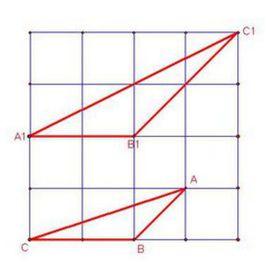
a=39,b=14,s=45一張方格紙上,上面畫著縱橫兩組平行線,相鄰平行線之間的距離都相等,這樣兩組平行線的交點,就是所謂格點。如果取一個格點做原點O,如圖1,取通過這個格點的橫向和縱向兩直線分別做橫坐標軸OX和縱坐標軸OY,並取原來方格邊長做單位長,建立一個坐標系。這時前面所說的格點,顯然就是縱橫兩坐標都是整數的那些點。如圖1中的O、P、Q、M、N都是格點。由於這個緣故,我們又叫格點為整點。
一個多邊形的頂點如果全是格點,這多邊形就叫做格點多邊形。有趣的是,這種格點多邊形的面積計算起來很方便,只要數一下圖形邊線上的點的數目及圖內的點的數目,就可用公式算出。
這個公式是皮克(Pick)在1899年給出的,被稱為“皮克定理”,這是一個實用而有趣的定理。
給定頂點坐標均是整點(或正方形格點)的簡單多邊形,皮克定理說明了其面積S和內部格點數目n、多邊形邊界上的格點數目s的關係:
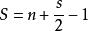 皮克定理
皮克定理驗證推導
因為所有簡單多邊形都可切割為一個三角形和另一個簡單多邊形。考慮一個簡單多邊形 P,及跟 P有一條共同邊的三角形 T。若 P符合皮克公式,則只要證明 P加上 T的 PT亦符合皮克公式(I),以及三角形符合皮克公式(II),就可根據數學歸納法,對於所有簡單多邊形皮克公式都是成立的。
多邊形
設P和T的共同邊上有c個格點。
P的面積: iP + bP/2 - 1
T的面積: iT + bT/2 - 1
PT的面積:
( iT + iP + c - 2) + ( bT- c + 2 + bP - c) /2 - 1 = iPT + bPT/2 - 1
三角形
證明分三部分:證明以下的圖形符合皮克定理:
所有平行於軸線的矩形;
以上述矩形的兩條鄰邊和對角線組成的直角三角形;
所有三角形(因為它們都可內接於矩形內,將矩形分割成原三角形和至多3個第二點提到的直角三角形)。
矩形
設矩形 R長邊短邊各有 m, n個格點:
AR = ( m-1)( n-1)
iR = ( m-2)( n-2)
bR = 2(m+n)-4
iR + bR/2 - 1 = ( m-2)( n-2) + (m+n) - 2 - 1 = mn - ( m + n) +1 = ( m-1)( n-1)
直角三角形
易見兩條鄰邊和對角線組成的兩個直角三角形全等,且 i, b相等。設其斜邊上有 c個格點。
b = m+ n+ c-3
i = (( m-2)( n-2) - c + 2)/2
i + b/2 - 1 = (( m-2)( n-2) - c + 2)/2 + ( m+ n+ c-3)/2 - 1 = ( m-2)( n-2)/2 + ( m+ n - 3)/2 = ( m-1)( n-1)/2
一般三角形
逆運用前面對2個多邊形的證明: 既然矩形符合皮克定理,直角三角形符合皮克定理。又前面證明到若P,T符合皮克公式,則 P加上T的PT亦符合皮克公式。 那么由於矩形可以分解成1個任意三角形和至多三個直角三角形。 於是顯然有,只有當這個任意三角形也符合皮克定理的時候,才會使得在直角三角形符合的同時,矩形也符合。
套用例子
證明Farey序列的一個神奇的性質:前一項的分母乘以後一項的分子,一定比前一項的分子與後一項分母之積大1。