歐幾里得的證明
歐幾里得在他的著作《幾何原本》(第九卷的定理20)提出了證明,大意如下:
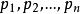 歐幾里得定理
歐幾里得定理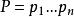 歐幾里得定理
歐幾里得定理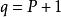 歐幾里得定理
歐幾里得定理對任何有限素數的集合 。在這裡將會證明最少存在一個集合中沒有的額外素數。令 和 。那么q是素數或者不是,二者必居其一:
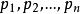 歐幾里得定理
歐幾里得定理1、如果q是素數,那么至少有一個素數不在有限素數集 中。
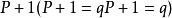 歐幾里得定理
歐幾里得定理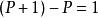 歐幾里得定理
歐幾里得定理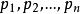 歐幾里得定理
歐幾里得定理2、如果q不是素數,那么存在一個素數因子p整除q,如果p在我們的有限素數集中, p必然整除 P(既然 P是素數有限集中所有素數的積);但是,已知 p整除 ,如果 p同時整除P和q, p必然整除 P和q之差—— 。但是沒有素數能整除1,即有p整除q就不存在 p整除P。因此p不在有限集 中。
這證明了:對於任何一個有限素數集,總存在一個素數不在其中。所以素數一定是無限的。
很多時候有人會錯誤地指出歐幾里得是用了反證法,他們假設證明起初考慮的是所有自然數的集合,或是集合內含有n個最小的素數,而不是任何任意的素數集合。歐幾里得證明用的不是反證法,而是證明了一個有限集合中沒有任何擁有特殊性質的元素。當中並沒有反論的部分,但集合中的任何元素都不可以整除1。
文獻中存在數個版本的歐幾里得證明,包括以下的:
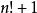 歐幾里得定理
歐幾里得定理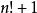 歐幾里得定理
歐幾里得定理正整數n的階乘n!可被2至 n的所有整數整除,這是由於它是這些數全部的乘積。因此 並不能被 2至 n(包括 n)的任何自然數所整除(所得的餘數皆為1)。因此 有兩個可能性:是素數,或者能被大於 n所整除。在任一個案中,對所有正整數n而言都存在最小一個比n大的素數。所以結論就是共有無限個素數。
歐拉的證明
另一個由瑞士數學家萊昂哈德·歐拉提出的證明,則使用了算術基本定理:每一個自然數都有一組獨一無二的素因子排列。設P為所有自然數的集合,歐拉寫下了:
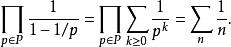 歐幾里得定理
歐幾里得定理第一條等式是由乘積中每一項的等比數列公式所得。而第二個等式則是用於黎曼ζ函式的歐拉乘積。為了證實此點,可把乘積分配進和裡面:
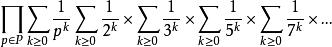 歐幾里得定理
歐幾里得定理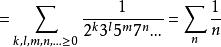 歐幾里得定理
歐幾里得定理在這個結果中,每一個素數積都出現了正好一次,因此由算術基本定理可得這個和等於所有自然數的和。
右邊的和是發散的調和級數。因此左邊的和也是發散的。由於乘積內每一個項都是有限的,所以其項數必須為無限;因此得出共有無限個素數。
埃爾德什的證明
 歐幾里得定理
歐幾里得定理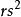 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理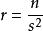 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理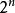 歐幾里得定理
歐幾里得定理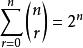 歐幾里得定理
歐幾里得定理埃爾德什·帕爾的第三種證明也是靠算術基本定理的。首先注意每一個自然數 都能被寫成獨一無二的 。其中 非平方數,或任何平方數的倍數(設 為能整除 的最大平方數,並使 )。此時假設素數的數量為有限,且其數量為 。由於每個素數只有一個非平方數的因子,所以根據算術基本定理,得出共有非平方數 個。(見組合#在集合中取出k項元素及 )
 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理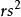 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理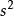 歐幾里得定理
歐幾里得定理現在把一個正整數 固定,並考慮1與 之間的自然數。 這些數每一個都能被寫成 ,其中 為非平方數, 為平方數,例如:
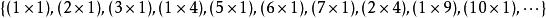 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理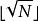 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理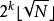 歐幾里得定理
歐幾里得定理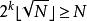 歐幾里得定理
歐幾里得定理集合中共有 個不同的數。每一個都是由非方數和比 小的平方數組成。這樣的平方數共有 (見高斯符號的取底符號)。然後把這些小於 的平方數乘積與其餘所有的非平方數相乘。這樣得出的數一共有 個,各不相同,因此它們包括了所有我們集合里的數,甚至更多。因此, 。
 歐幾里得定理
歐幾里得定理由於此不等式對足夠大的 並不成立,因此必須存在無限個素數。
近期的證明
皮納西科
胡安·帕布洛·皮納西科(Juan Pablo Pinasco)寫下了以下的證明。
 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理設 為最小的 個素數。然後根據容斥原理可得,少於或等如 又同時能被那些素數中其中一個整除的正整數的個數為
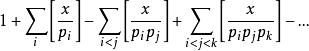 歐幾里得定理
歐幾里得定理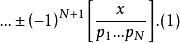 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理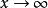 歐幾里得定理
歐幾里得定理把全式除以 ,並且讓 ,得
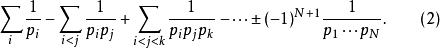 歐幾里得定理
歐幾里得定理上式可被改寫為
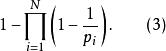 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理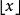 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理若除了 以外不存在其他素數的話,則式(1)與 相等,而式(2)則等於 ,但很明顯地式(3)並不等於1。因此除了以外必須要存在其他素數。
黃
俊浩·彼得·黃(Junho Peter Whang)於2010年發表了使用反證法的證明。設{\displaystyle k}為任何正整數,{\displaystyle p}為素數。根據勒讓德定理,則可得:
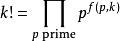 歐幾里得定理
歐幾里得定理其中
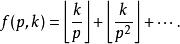 歐幾里得定理
歐幾里得定理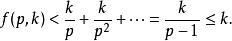 歐幾里得定理
歐幾里得定理但若只存在有限個素數,則
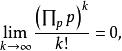 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理(上式分子呈單指數增長,但斯特靈公式指出分母的增長速度比分子快),這樣就違反了每一個的分子要比分母大的這一點。
塞達克
 歐幾里得定理
歐幾里得定理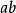 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理菲利浦·塞達克(Filip Saidak)給出了以下的證明,當中沒有用到歸謬法(而大部分歐幾里得定理的證明都用了,包括歐幾里得自己的證明),而同時不需要用到歐幾里得引理,也就是若素數整除則也必能整除或。證明如下:
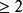 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理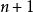 歐幾里得定理
歐幾里得定理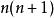 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理由於每個自然數(
)最少擁有一個素因子,所以兩個相鄰數字和必定沒有共同因子,而乘積則比數字本身擁有更多因子。因此普洛尼克數的鏈:1×2 = 2 {2}, 2×3 = 6 {2, 3}, 6×7 = 42 {2,3, 7}, 42×43 = 1806 {2,3,7, 43}, 1806×1807 = 3263443 {2,3,7,43, 13,139}, · · ·
提供了一組素數集合無限增長的數列。
使用π的無理性的證明
以歐拉乘積來表示π的萊布尼茨公式可得
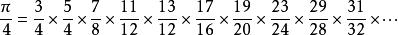 歐幾里得定理
歐幾里得定理乘積的分子為奇數的素數,而每一個分母則是最接近分子的4的倍數。
若存在的素數是有限的話,上式所展示的就是π是一個有理數,而分母是所有與素數多1或少1的4的倍數的乘積,而這點違反了π實際上是無理數的這一點。
使用資訊理論的證明
 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理設只存在素數()。由算術基本定理可得,任何正整數都能被寫成:
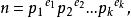 歐幾里得定理
歐幾里得定理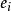 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理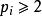 歐幾里得定理
歐幾里得定理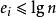 歐幾里得定理
歐幾里得定理其中非負自然數與素數的有限集合就足夠重構任何數字。由於所有都遵守,因此可得所有\(其中{\displaystyle \lg }代表底數為2的對數)。
 歐幾里得定理
歐幾里得定理由此可得的編碼大小(使用大O符號):
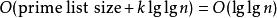 歐幾里得定理
歐幾里得定理位元。
 歐幾里得定理
歐幾里得定理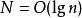 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理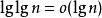 歐幾里得定理
歐幾里得定理 歐幾里得定理
歐幾里得定理(其中prime list size為素數集合的大小)這編碼比直接用二進制代表要有效得多,二進制的話需要位元。無損數據壓縮的一個已被確立的結果指出,一般不可能把位元的信息壓縮到少於位元。由於,所以當足夠大時,以上的這個表示不成立。
因此,素數的數量必不能為有限。
參閱
•狄利克雷定理
•素數定理
