證明
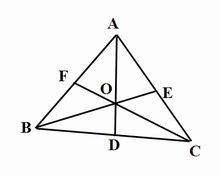 燕尾定理
燕尾定理證法1
下面的是第一種方法:利用分比性質(若a÷b=c÷d,則(a-b)÷b=(c-d)÷d,
b≠0,d≠0,)
註:∵(a-b)÷b=a÷b-b÷b=a÷b-1,
(c-d)÷d=c÷d-d÷d=c÷d-1,
a/b=c/d
∴(a-b)÷b=(c-d)÷d
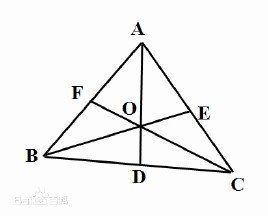
∵△ABD與△ACD同高
∴S△ABD:S△ACD=BD:CD
同理,S△OBD:S△OCD=BD:CD
利用分比性質,得
S△ABD-S△OBD:S△ACD-S△OCD=BD:CD
即S△AOB:S△AOC=BD:CD
命題得證。(由此可得:若X:Y=a:b,X1:Y1=a:b;則(X±X1):(Y±Y1)=a:b.其中Y、Y1≠0,Y≠Y1且Y-≠Y1)
證法2
下面的是第二種方法:相似三角形法
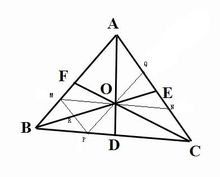 證法1圖
證法1圖已知:△ABC的兩條中線AD、CF相交於點O,連線並延長BO,交AC於點E。
求證:AE=CE 證明:
過點O作MN∥BC,,交AB於點M,AC於點N;
過點O作PQ∥AB,交BC於點P,交AC於點Q。
∵MN∥BC
∴△AMO∽△ABD,△ANO∽△ACD
∴MO:BD=AO:AD,NO:CD=AO:AD
∴MO:BD=NO:CD
∵AD是△ABC的一條中線
∴BD=CD
∴MO=NO
∵PQ∥AB
∴△CPO∽△CBF,△CQO∽△CAF
∴PO:BF=CO:CF,QO:AF=CO:CF
∴PO:BF=QO:AF
∵CF是△ABC的一條中線
∴AF=BF
∴PO=QO
∵MO=NO,∠MOP=∠NOQ,PO=QO
∴△MOP≌△NOQ(SAS)
∴∠MPO=∠NQO
∴MP∥AC(內錯角相等,兩條直線平行)
∴△BMR∽△BAE(R為MP與BO的交點),△BPR∽△BCE
∴MR:AE=BR:BE,PR:CE=BR:BE
∴MR:AE=PR:CE
∵MN∥BC,PQ∥AB
∴四邊形BMOP是平行四邊形
∴MR=PR(平行四邊形的對角線互相平分)
∴AE=CE
命題得證。
證法3
下面的是第三種方法:面積法
已知:△ABC的兩條中線AD、CF相交於點O,連線並延長BO,交AC於點E。
求證:AE=CE
證明:
如圖,
∵點D是BC的中點,點F是AB的中點
∴S△CAD = S△BAD,S△COD = S△BOD
∴S△CAD - S△COD = S△BAD - S△BOD
即S△AOC(綠) = S△AOB(紅)
∵S△ACF = S△BCF,S△AOF = S△BOF
∴S△ACF - S△AOF = S△BCF - S△BOF
即S△AOC(綠) = S△BOC(藍)
∴S△AOB(紅) = S△BOC(藍)
∵S△AOE:S△AOB(紅) = OE:OB,S△COE:S△BOC(藍) = OE:OB
∴S△AOE:S△AOB(紅) = S△COE:S△BOC(藍)
∵S△AOB(紅) = S△BOC(藍)
∴S△AOE = S△COE
∴AE=CE
命題得證。
證法4
下面的是第四種方法:中位線法
已知:△ABC的兩條中線AD、CF相交於點O,連線並延長BO,交AC於點E。
求證:AE=CE
證明:
如圖,延長OE到點G,使OG=OB。
∵OG=OB
∴點O是BG的中點
又∵點D是BC的中點
∴OD是△BGC的一條中位線
∴AD∥CG(三角形的中位線平行於第三邊,且等於第三邊的一半)
∵點O是BG的中點,點F是AB的中點
∴OF是△BGA的一條中位線
∴CF∥AG
∵AD∥CG,CF∥AG
∴四邊形AOCG是平行四邊形
∴AC、OG互相平分
∴AE=CE
命題得證。
證法5:因為ABCO是凹四邊形,根據共邊比例定理,命題得證
推廣
四邊形ABCD(不一定是凸四邊形),設AC,BD相交於E則有BE :DE=S△ABC :S△ADC
證明:∵S△ABC=S△ABE+S△BEC
S△ADC=S△AED+S△CED.
又∵S△ABE:S△AED=S△BEC:S△CED=BE:ED(∵高相等). ∴S△ABE+S△BEC:S△AED+S△CED=S△ABC :S△ADC=BE:ED
此定理是面積法最重要的定理之一.